Arvores de Regressão

Author

Ricardo Accioly

Published

November 11, 2025

Bibliotecas

Carregando os dados

data("Boston")
names(Boston)
#>  [1] "crim"    "zn"      "indus"   "chas"    "nox"     "rm"      "age"    
#>  [8] "dis"     "rad"     "tax"     "ptratio" "black"   "lstat"   "medv"
describe(Boston)
#>         vars   n   mean     sd median trimmed    mad    min    max  range  skew
#> crim       1 506   3.61   8.60   0.26    1.68   0.33   0.01  88.98  88.97  5.19
#> zn         2 506  11.36  23.32   0.00    5.08   0.00   0.00 100.00 100.00  2.21
#> indus      3 506  11.14   6.86   9.69   10.93   9.37   0.46  27.74  27.28  0.29
#> chas       4 506   0.07   0.25   0.00    0.00   0.00   0.00   1.00   1.00  3.39
#> nox        5 506   0.55   0.12   0.54    0.55   0.13   0.38   0.87   0.49  0.72
#> rm         6 506   6.28   0.70   6.21    6.25   0.51   3.56   8.78   5.22  0.40
#> age        7 506  68.57  28.15  77.50   71.20  28.98   2.90 100.00  97.10 -0.60
#> dis        8 506   3.80   2.11   3.21    3.54   1.91   1.13  12.13  11.00  1.01
#> rad        9 506   9.55   8.71   5.00    8.73   2.97   1.00  24.00  23.00  1.00
#> tax       10 506 408.24 168.54 330.00  400.04 108.23 187.00 711.00 524.00  0.67
#> ptratio   11 506  18.46   2.16  19.05   18.66   1.70  12.60  22.00   9.40 -0.80
#> black     12 506 356.67  91.29 391.44  383.17   8.09   0.32 396.90 396.58 -2.87
#> lstat     13 506  12.65   7.14  11.36   11.90   7.11   1.73  37.97  36.24  0.90
#> medv      14 506  22.53   9.20  21.20   21.56   5.93   5.00  50.00  45.00  1.10
#>         kurtosis   se
#> crim       36.60 0.38
#> zn          3.95 1.04
#> indus      -1.24 0.30
#> chas        9.48 0.01
#> nox        -0.09 0.01
#> rm          1.84 0.03
#> age        -0.98 1.25
#> dis         0.46 0.09
#> rad        -0.88 0.39
#> tax        -1.15 7.49
#> ptratio    -0.30 0.10
#> black       7.10 4.06
#> lstat       0.46 0.32
#> medv        1.45 0.41

Conhecendo as variáveis

  • crim: taxa de criminalidade per capita por cidade.

  • zn: proporção de terrenos residenciais zoneados para lotes acima de 25.000 pés quadrados.

  • indus: proporção de acres de negócios não varejistas por cidade.

  • chas: variável fictícia do rio Charles (= 1 se o trato limita o rio; 0 caso contrário). nox concentração de óxidos de nitrogênio (partes por 10 milhões).

  • rm: número médio de cômodos por habitação.

  • age: proporção de unidades ocupadas pelo proprietário construídas antes de 1940.

  • dis: média ponderada das distâncias até cinco centros de emprego de Boston.

  • rad: índice de acessibilidade a rodovias radiais. tax taxa de imposto sobre a propriedade do valor total por $ 10.000.

  • ptratio: proporção aluno-professor por cidade.

  • black: 1000(Bk−0,63)21000(Bk−0,63)2 onde BkBk é a proporção de negros por cidade.

  • lstat: status inferior da população (por cento).

  • medv: valor médio das casas ocupadas pelo proprietário em $ 1000s.

Selecionando os dados

dados <- Boston 
extrato <- dados %>% select(medv, nox, rm)  
summary(extrato)
#>       medv            nox               rm       
#>  Min.   : 5.00   Min.   :0.3850   Min.   :3.561  
#>  1st Qu.:17.02   1st Qu.:0.4490   1st Qu.:5.886  
#>  Median :21.20   Median :0.5380   Median :6.208  
#>  Mean   :22.53   Mean   :0.5547   Mean   :6.285  
#>  3rd Qu.:25.00   3rd Qu.:0.6240   3rd Qu.:6.623  
#>  Max.   :50.00   Max.   :0.8710   Max.   :8.780
boxplot(extrato$medv)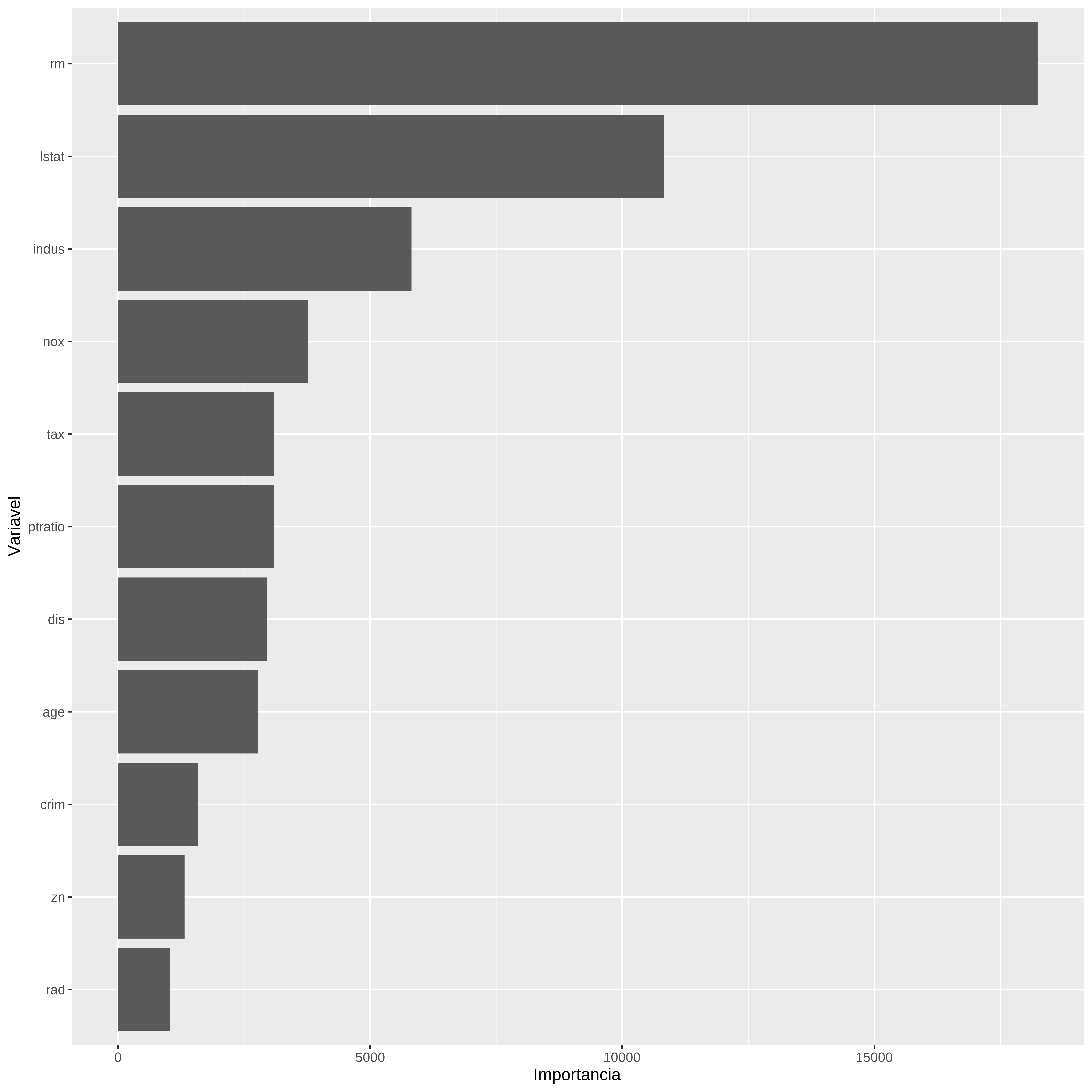

Visualizando os dados

## Distribuição de dados na maior parte simétrica com valores na cauda direta 
## maior do que o esperado para uam distribuição simétrica
ggplot(extrato, aes(x=medv)) +
  geom_histogram(bins = round(1+3.322*log10(nrow(extrato)),0))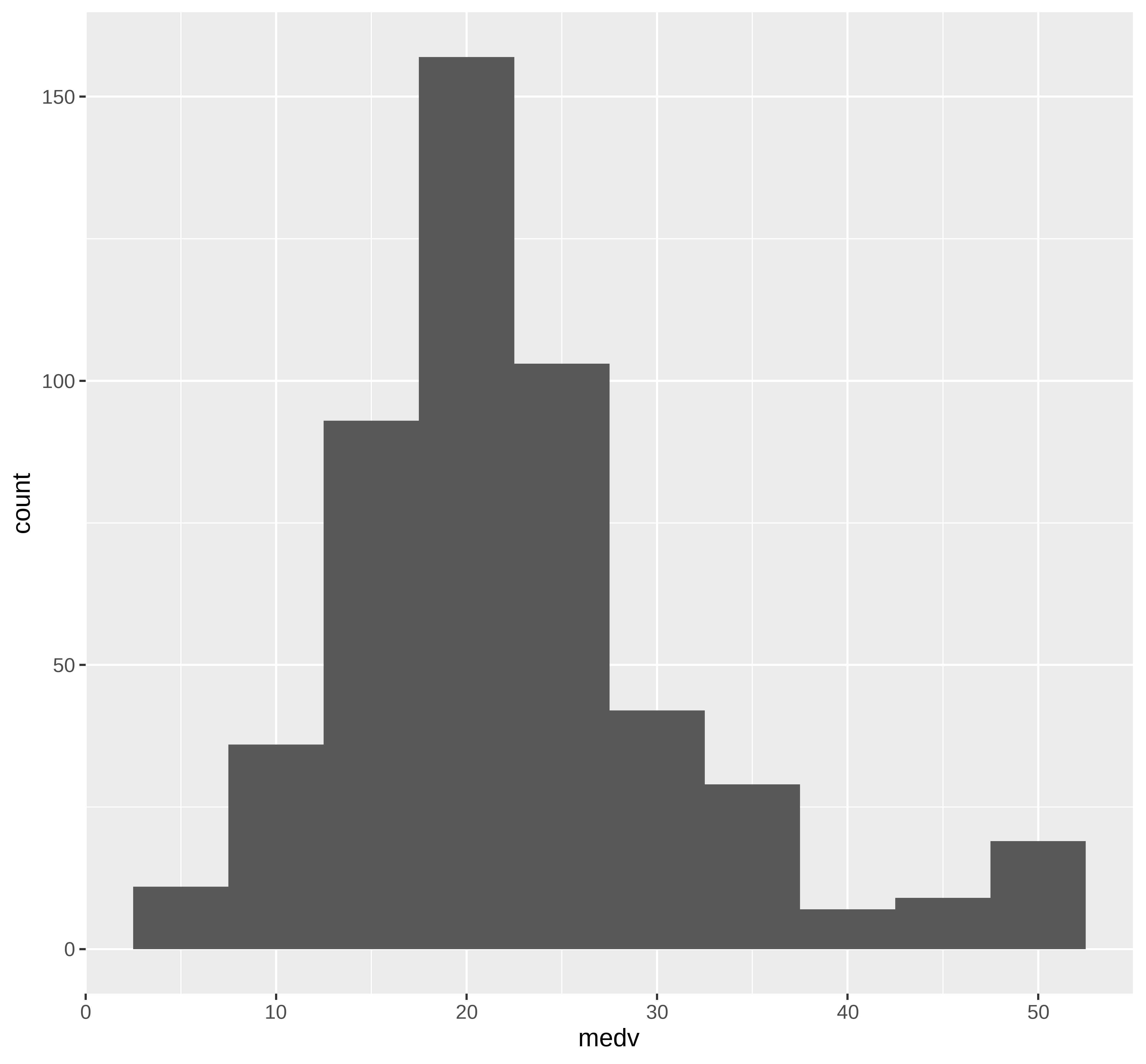

## Grafico de dispersão nox vs rm 
ggplot(extrato, aes(x=rm, y=nox)) + 
  geom_point()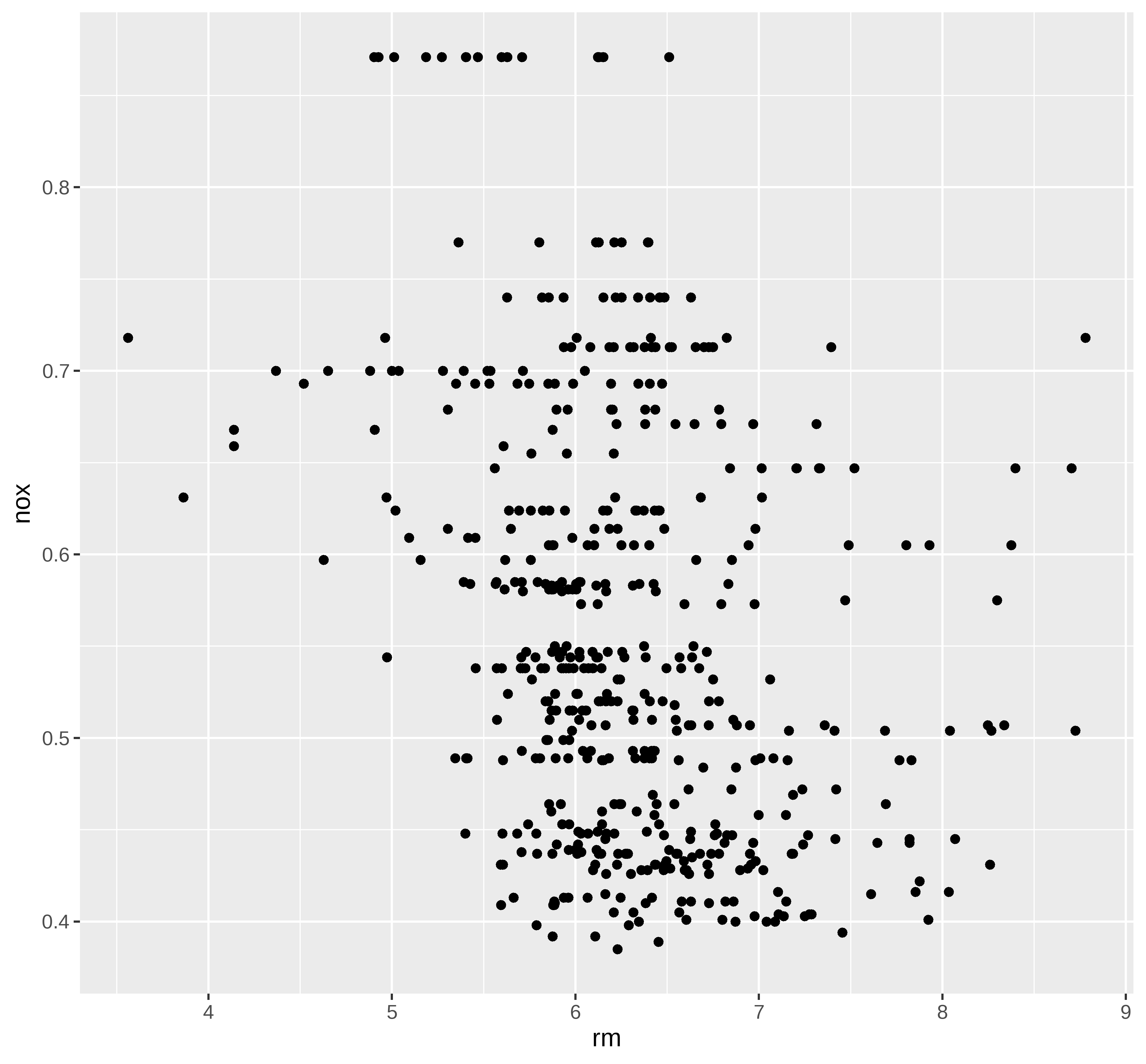

Arvore de Regressão

Na biblioteca rpart as arvores de regressão são obtidas usando o método anova. Existem alguns controles que podem ser feitos nos parametros da arvore.

Neste exemplo só definimos o menor conjunto de dados numa partição (minsplit) e o parametro de complexidade cp. Qualquer partição/divisão que não melhore o ajuste por um fator de cp não é tentada. Por exemplo, com a partição pela anova, isso significa que o R-quadrado geral deve aumentar pelo valor de cp a cada etapa. O principal papel deste parâmetro é economizar tempo de computação podando divisões que obviamente não valem a pena. Essencialmente, o usuário informa ao programa que qualquer divisão que não melhore o ajuste pelo cp, provavelmente será podada por validação cruzada, e que, portanto, não é necessário persegui-lo.

##Usando rpart para desenvolver a arvore  
arvreg <- rpart(medv ~ ., 
                data=extrato,
                method="anova", #para arvore de regressão
                control=rpart.control(minsplit=30,cp=0.06))
arvreg
#> n= 506 
#> 
#> node), split, n, deviance, yval
#>       * denotes terminal node
#> 
#> 1) root 506 42716.300 22.53281  
#>   2) rm< 6.941 430 17317.320 19.93372  
#>     4) nox>=0.6695 97  2214.391 13.73918 *
#>     5) nox< 0.6695 333 10296.590 21.73814 *
#>   3) rm>=6.941 76  6059.419 37.23816  
#>     6) rm< 7.437 46  1899.612 32.11304 *
#>     7) rm>=7.437 30  1098.850 45.09667 *
rpart.plot(arvreg)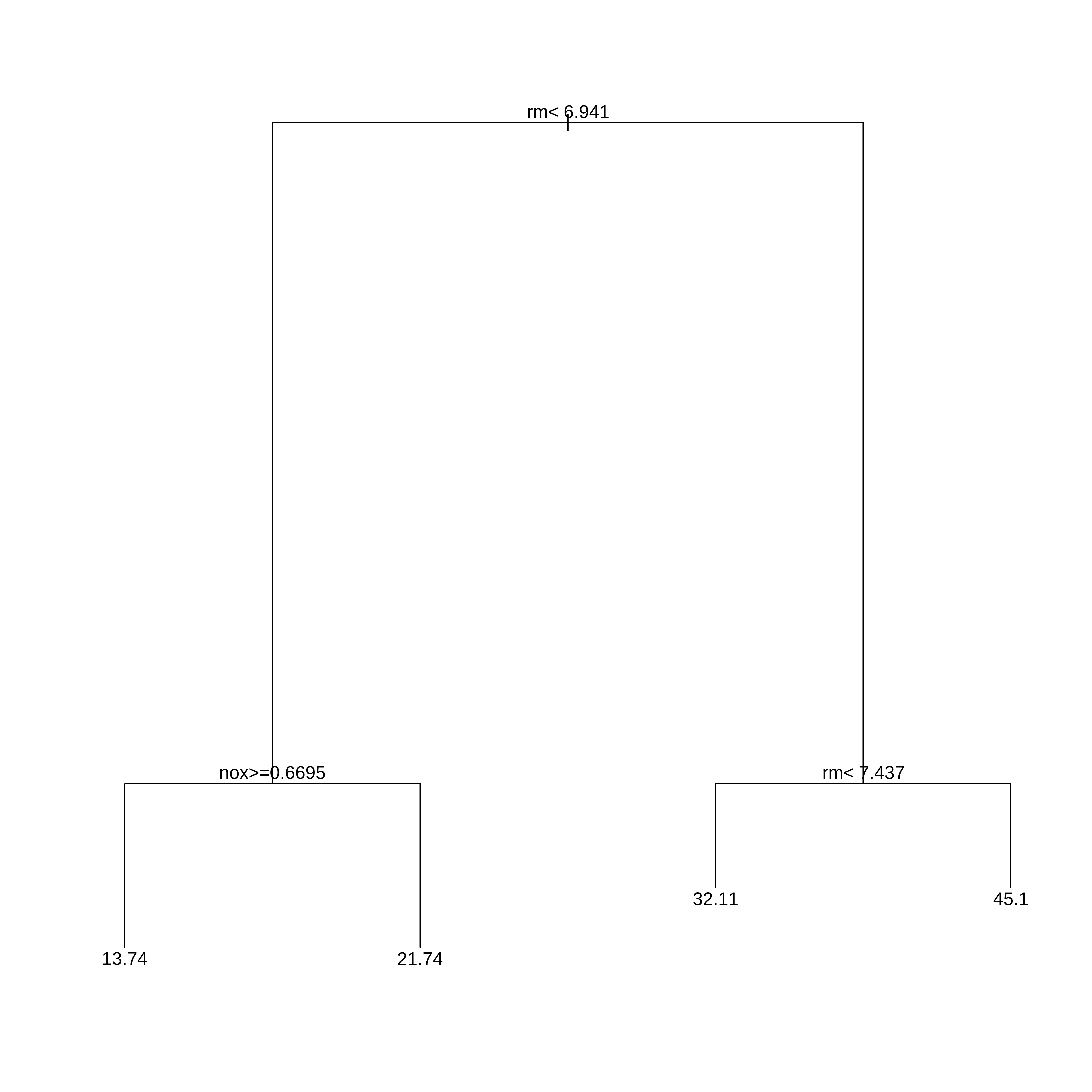

Segmentos

A partir da árvore obtida no item anterior podemos fazer uma representação gráfica das partições obtidas.

ggplot(extrato, aes(x=rm, y=nox)) + 
  geom_point() +
  geom_segment(aes(x = 0, y = 0.6695, xend = 6.941, yend = 0.6695), 
               linetype="dashed", color="red", size=1) +
  geom_vline(xintercept = 6.941, linetype="dashed", color="red", size=1) +
  geom_vline(xintercept = 7.437, linetype="dashed", color="red", size=1)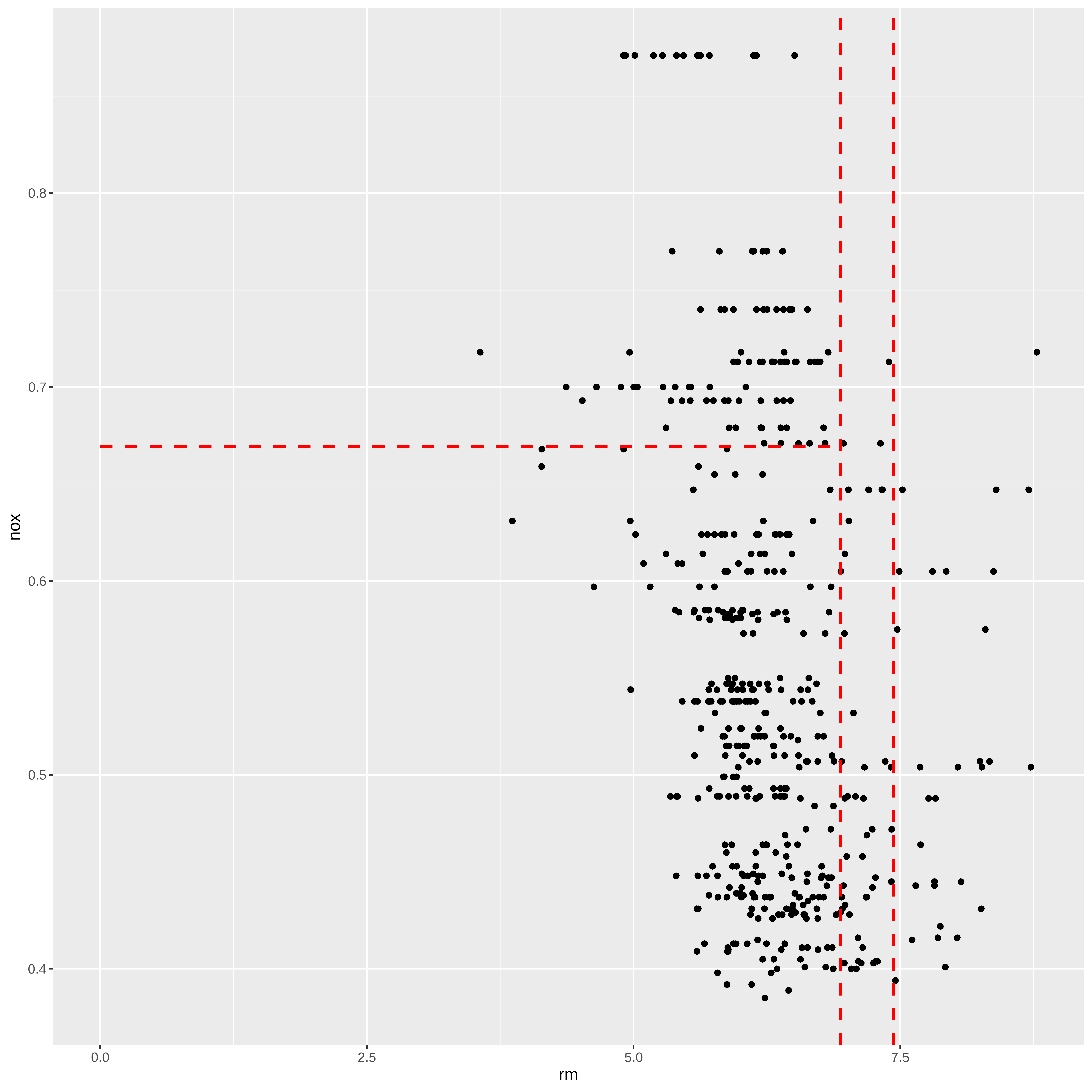 

  # scale_y_continuous(limits = c(0.3, 1)) +

Treino e Teste com todas as variáveis

Agora vamos trabalhar com o conjunto completo criando um conjunto de treino e teste.

## Vamos criar os conjuntos de treino teste e desenvolver a arvore 
## com todas as variáveis.
set.seed(2025)
indice <- createDataPartition(dados$medv, times=1, p=0.75, list=FALSE)
conj_treino <- dados[indice,]
conj_teste <- dados[-indice,]
head(conj_treino)
#>       crim   zn indus chas   nox    rm  age    dis rad tax ptratio  black lstat
#> 2  0.02731  0.0  7.07    0 0.469 6.421 78.9 4.9671   2 242    17.8 396.90  9.14
#> 6  0.02985  0.0  2.18    0 0.458 6.430 58.7 6.0622   3 222    18.7 394.12  5.21
#> 7  0.08829 12.5  7.87    0 0.524 6.012 66.6 5.5605   5 311    15.2 395.60 12.43
#> 8  0.14455 12.5  7.87    0 0.524 6.172 96.1 5.9505   5 311    15.2 396.90 19.15
#> 10 0.17004 12.5  7.87    0 0.524 6.004 85.9 6.5921   5 311    15.2 386.71 17.10
#> 11 0.22489 12.5  7.87    0 0.524 6.377 94.3 6.3467   5 311    15.2 392.52 20.45
#>    medv
#> 2  21.6
#> 6  28.7
#> 7  22.9
#> 8  27.1
#> 10 18.9
#> 11 15.0
head(conj_teste)
#>       crim   zn indus chas   nox    rm   age    dis rad tax ptratio  black
#> 1  0.00632 18.0  2.31    0 0.538 6.575  65.2 4.0900   1 296    15.3 396.90
#> 3  0.02729  0.0  7.07    0 0.469 7.185  61.1 4.9671   2 242    17.8 392.83
#> 4  0.03237  0.0  2.18    0 0.458 6.998  45.8 6.0622   3 222    18.7 394.63
#> 5  0.06905  0.0  2.18    0 0.458 7.147  54.2 6.0622   3 222    18.7 396.90
#> 9  0.21124 12.5  7.87    0 0.524 5.631 100.0 6.0821   5 311    15.2 386.63
#> 19 0.80271  0.0  8.14    0 0.538 5.456  36.6 3.7965   4 307    21.0 288.99
#>    lstat medv
#> 1   4.98 24.0
#> 3   4.03 34.7
#> 4   2.94 33.4
#> 5   5.33 36.2
#> 9  29.93 16.5
#> 19 11.69 20.2

Arvore de Regressão com caret

Aqui vamos usar a biblioteca caret que tem umas facilidades para otimização do cp e apresentação dos resultados

set.seed(2025)
## Otimizamos o valor de cp usando um 10-fold cv
# O parametro tuneLength diz para o algoritmo escolher diferentes valores para cp
# O parametro tuneGrid permite decidir que valores cp deve assumir enquanto que o
# tuneLength somente limita o número default de parametros que se usa.
arvreg2 <- train(medv ~ . , data = conj_treino, method = "rpart",
                 trControl = trainControl("cv", number = 10),
                 tuneGrid = data.frame(cp = seq(0.01,0.10, length.out=100)) 
                 )
# Mostra a acurácia vs cp (parametro de complexidade)
plot(arvreg2)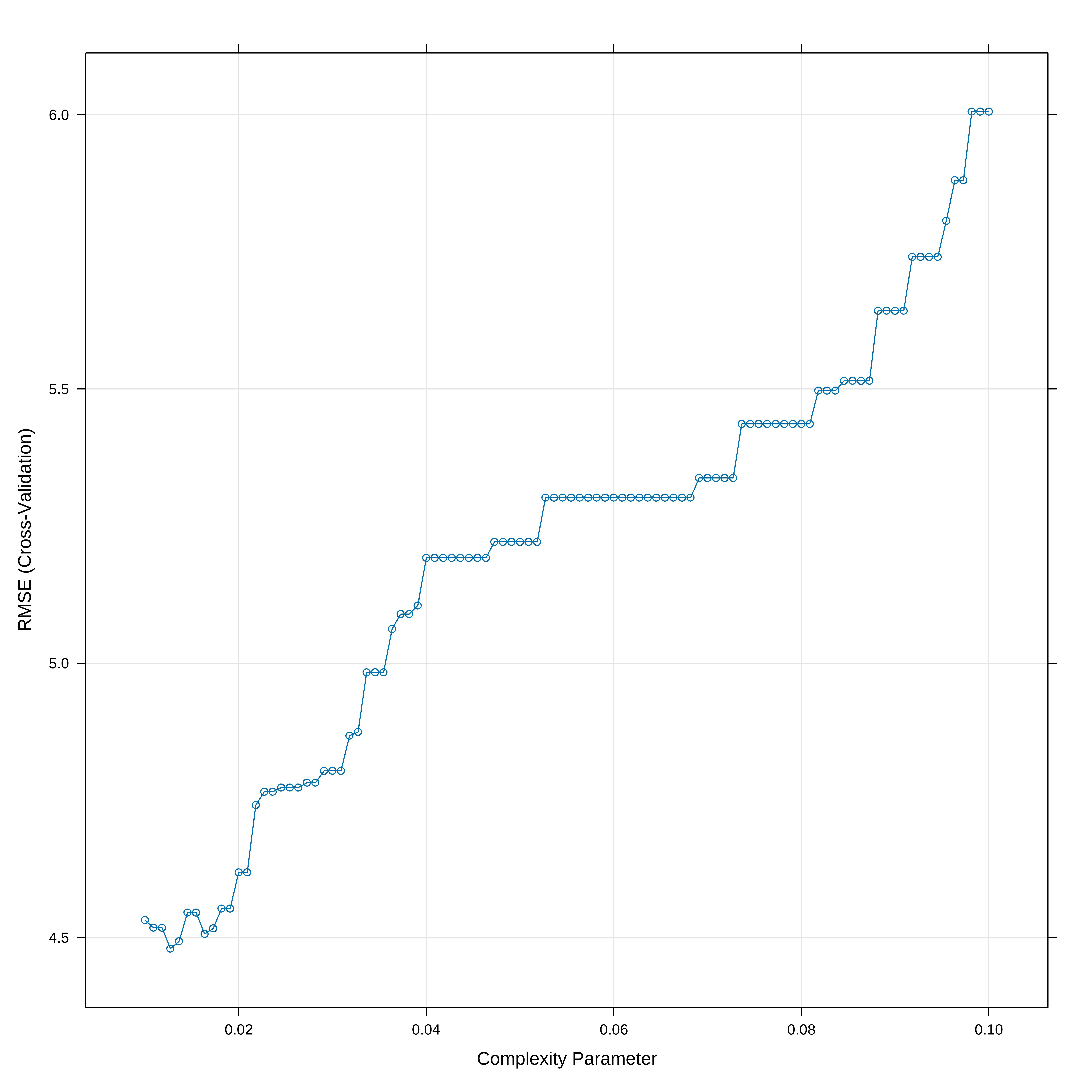

## Indica o melhor valor de cp
arvreg2$bestTune
#>           cp
#> 2 0.01090909

Desenhando a Árvore

## Apresenta o modelo final de arvore ajustado
## usando o rpart.plot
rpart.plot(arvreg2$finalModel)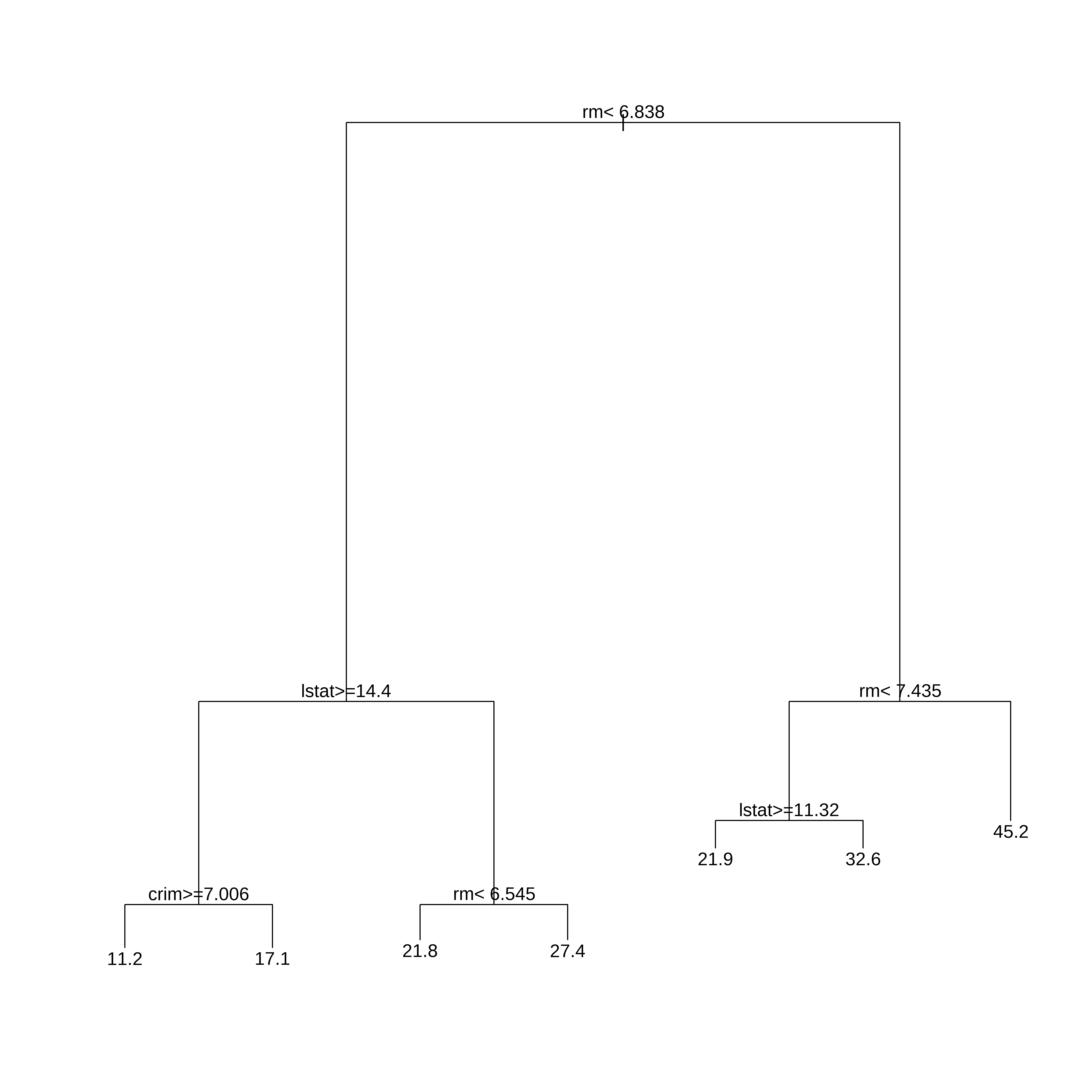

Gráfico de importancia das variáveis

A importancia das variáveis é calculada com base nos resultados das melhores partições

# Gráfico de Importância de variável
var_imp <- varImp(arvreg2) 
var_imp$importance %>%
  rownames_to_column(var = "Variável") %>%
  ggplot(aes(x = reorder(Variável, Overall), y = Overall)) +
  geom_col(fill = "steelblue") +
  coord_flip() +
  labs(title = "Importância das Variáveis na Árvore de Regressão",
       x = "Variável",
       y = "Importância (Overall)") +
  theme_minimal()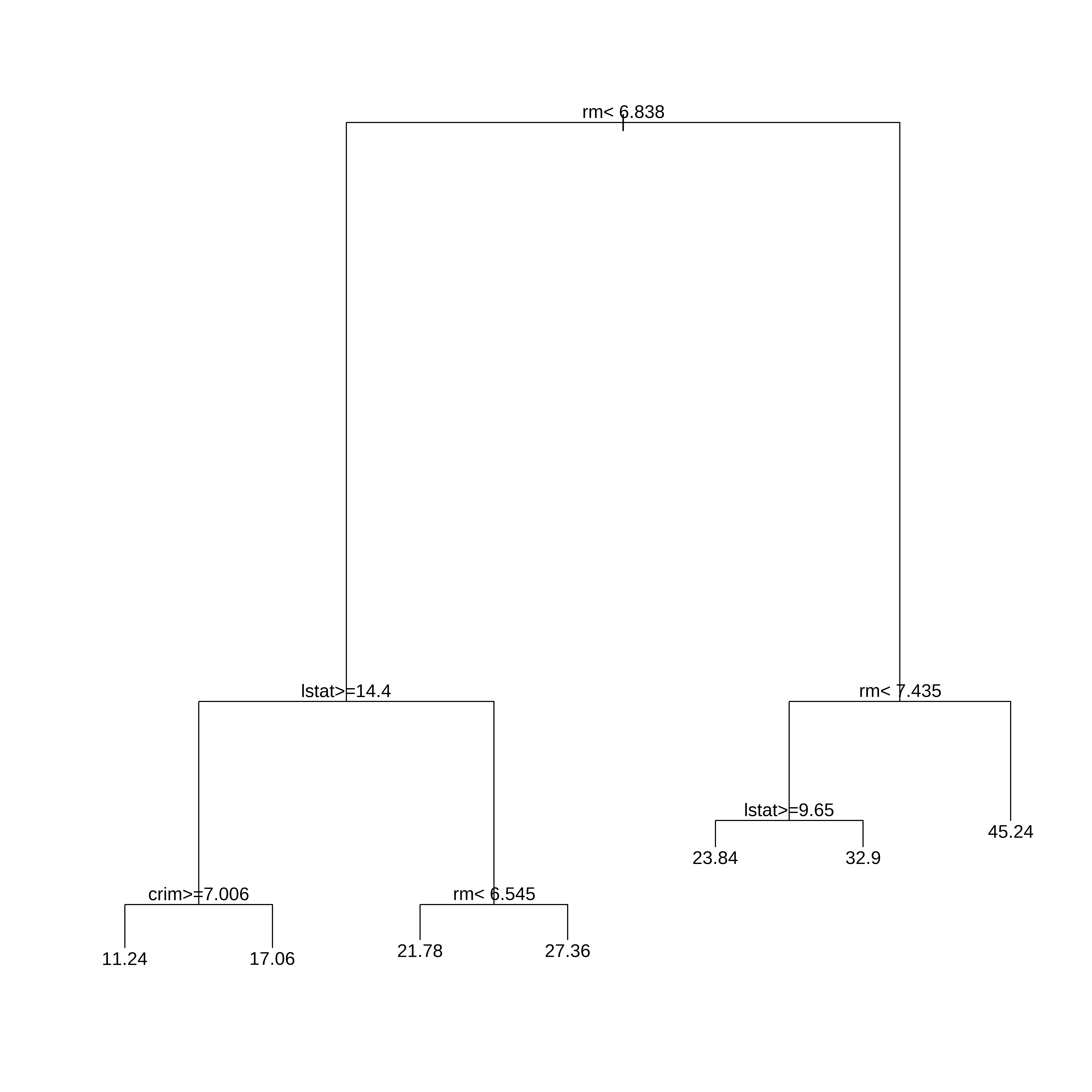

Previsões

# Regras de Decisão
arvreg2$finalModel
#> n= 381 
#> 
#> node), split, n, deviance, yval
#>       * denotes terminal node
#> 
#>  1) root 381 29517.3100 22.24934  
#>    2) rm< 7.0105 337 14500.6500 20.17745  
#>      4) lstat>=14.4 133  2641.8500 14.88271  
#>        8) nox>=0.607 84  1154.7830 12.88571  
#>         16) lstat>=19.645 45   393.3764 10.63111 *
#>         17) lstat< 19.645 39   268.7236 15.48718 *
#>        9) nox< 0.607 49   577.8082 18.30612 *
#>      5) lstat< 14.4 204  5699.3640 23.62941  
#>       10) rm< 6.543 156  3036.0710 22.16090  
#>         20) dis>=1.68515 149  1307.6110 21.81141 *
#>         21) dis< 1.68515 7  1322.8800 29.60000 *
#>       11) rm>=6.543 48  1233.5100 28.40208  
#>         22) lstat>=5.195 29   213.9524 26.04828 *
#>         23) lstat< 5.195 19   613.6495 31.99474 *
#>    3) rm>=7.0105 44  2489.9250 38.11818  
#>      6) rm< 7.435 26   382.4815 32.73846 *
#>      7) rm>=7.435 18   268.0578 45.88889 *
# Fazendo Previsões
previsao2 <- arvreg2 %>% predict(conj_teste)
head(previsao2)
#>        1        3        4        5        9       19 
#> 31.99474 32.73846 31.99474 32.73846 18.30612 21.81141
# Calcula os erros de previsão
RMSE(previsao2, conj_teste$medv)
#> [1] 4.882214

Vamos comparar com Regressão Multipla

library(leaps)
## Cria uma função de predição para o leaps
predict.regsubsets <- function(object,newdata,id,...){
  form <- as.formula(object$call[[2]])
  mat <- model.matrix(form,newdata)
  coefi <- coef(object,id=id)
  mat[,names(coefi)]%*%coefi
}
set.seed(2025)
envelopes <- sample(rep(1:5,length=nrow(conj_treino)))
table(envelopes)
#> envelopes
#>  1  2  3  4  5 
#> 77 76 76 76 76
erro_cv <- matrix(NA,5,13)
for(k in 1:5){
  melh_ajus <- regsubsets(medv ~ ., data=conj_treino[envelopes!=k,], 
                          nvmax=13,method="forward")
  for(i in 1:13){
    prev <- predict(melh_ajus, conj_treino[envelopes==k,],id=i)
    erro_cv[k,i] <- mean( (conj_treino$medv[envelopes==k]-prev)^2)
  }
}
rmse_cv <- sqrt(apply(erro_cv,2,mean))  # Erro medio quadratico de cada modelo
plot(rmse_cv,pch=19,type="b")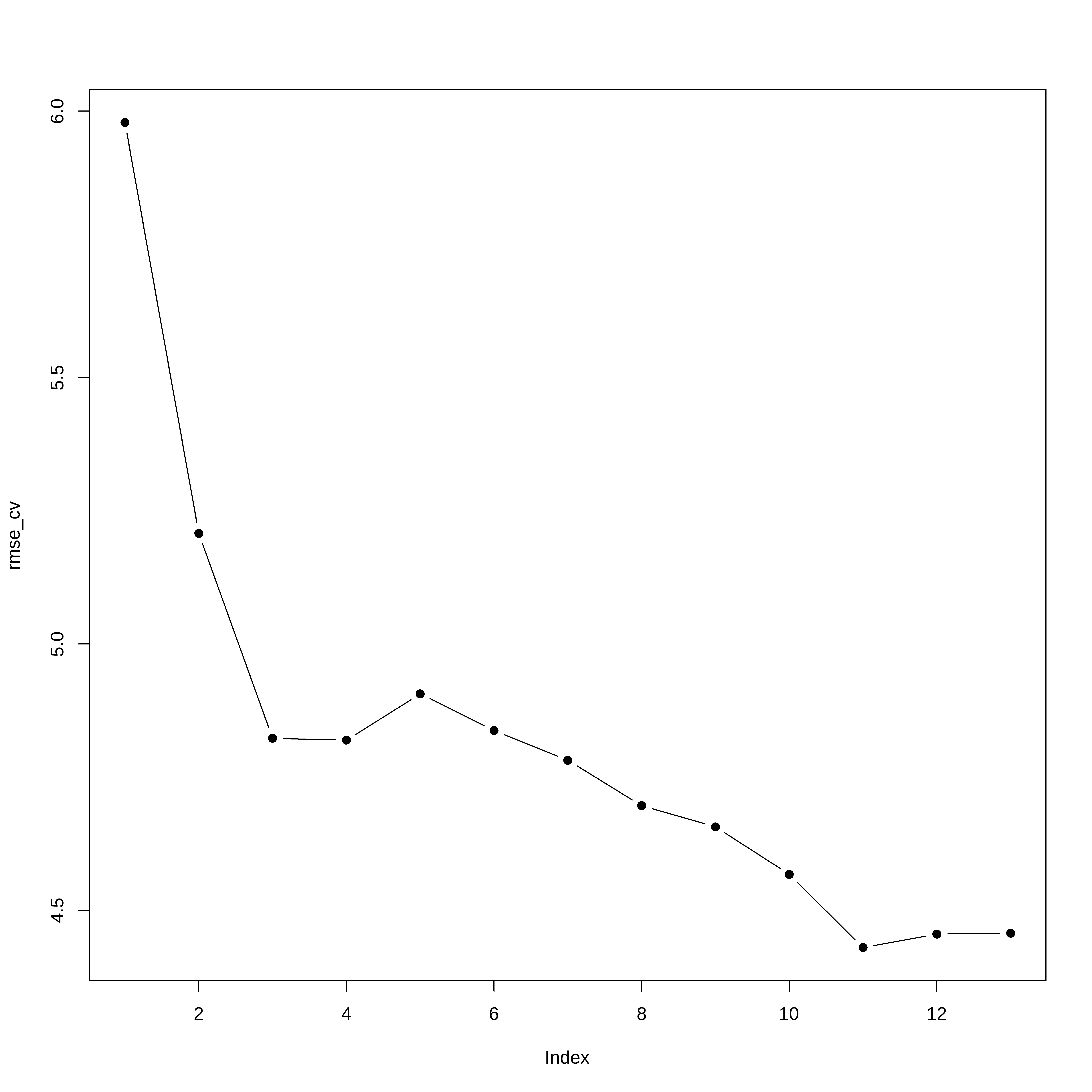

Obtem a fórmula do modelo

coef(melh_ajus, 11)
#>   (Intercept)          crim            zn          chas           nox 
#>  34.693940504  -0.124555425   0.050468728   4.160779593 -21.520063917 
#>            rm           dis           rad           tax       ptratio 
#>   4.179728433  -1.594068072   0.357136658  -0.013259547  -0.837573459 
#>         black         lstat 
#>   0.008077009  -0.500287649

Teste com o conjunto de teste

previsao3 <- predict(melh_ajus, conj_teste, 11) 
RMSE(previsao3, conj_teste$medv)
#> [1] 5.519325

E se usarmos outra semente?

## Vamos criar os conjuntos de treino teste e desenvolver a arvore 
## com todas as variáveis.
set.seed(23)
indice <- createDataPartition(dados$medv, times=1, p=0.75, list=FALSE)
conj_treino <- dados[indice,]

arvreg1s <- rpart(medv ~ ., 
                data=conj_treino,
                method="anova", #para arvore de regressão
                control=rpart.control(minsplit=30,cp=0.01))
arvreg1s
#> n= 381 
#> 
#> node), split, n, deviance, yval
#>       * denotes terminal node
#> 
#>  1) root 381 31257.8400 22.41496  
#>    2) rm< 6.92 321 11786.7500 19.74361  
#>      4) lstat>=14.4 133  2558.5280 14.88722  
#>        8) crim>=6.99237 59   866.3051 11.96949 *
#>        9) crim< 6.99237 74   789.4865 17.21351 *
#>      5) lstat< 14.4 188  3872.3890 23.17926  
#>       10) lstat>=5.51 165  2166.8920 22.28970  
#>         20) lstat>=9.675 86   527.0414 20.76977 *
#>         21) lstat< 9.675 79  1224.8950 23.94430 *
#>       11) lstat< 5.51 23   638.2548 29.56087 *
#>    3) rm>=6.92 60  4925.2370 36.70667  
#>      6) rm< 7.437 39  1510.0630 31.43077  
#>       12) ptratio>=18.55 10   750.6440 25.84000 *
#>       13) ptratio< 18.55 29   339.0703 33.35862 *
#>      7) rm>=7.437 21   313.5495 46.50476 *
## Colocar as duas arvores lado a lado
par(mfrow=c(1,2))
rpart.plot(arvreg1s)
rpart.plot(arvreg2$finalModel)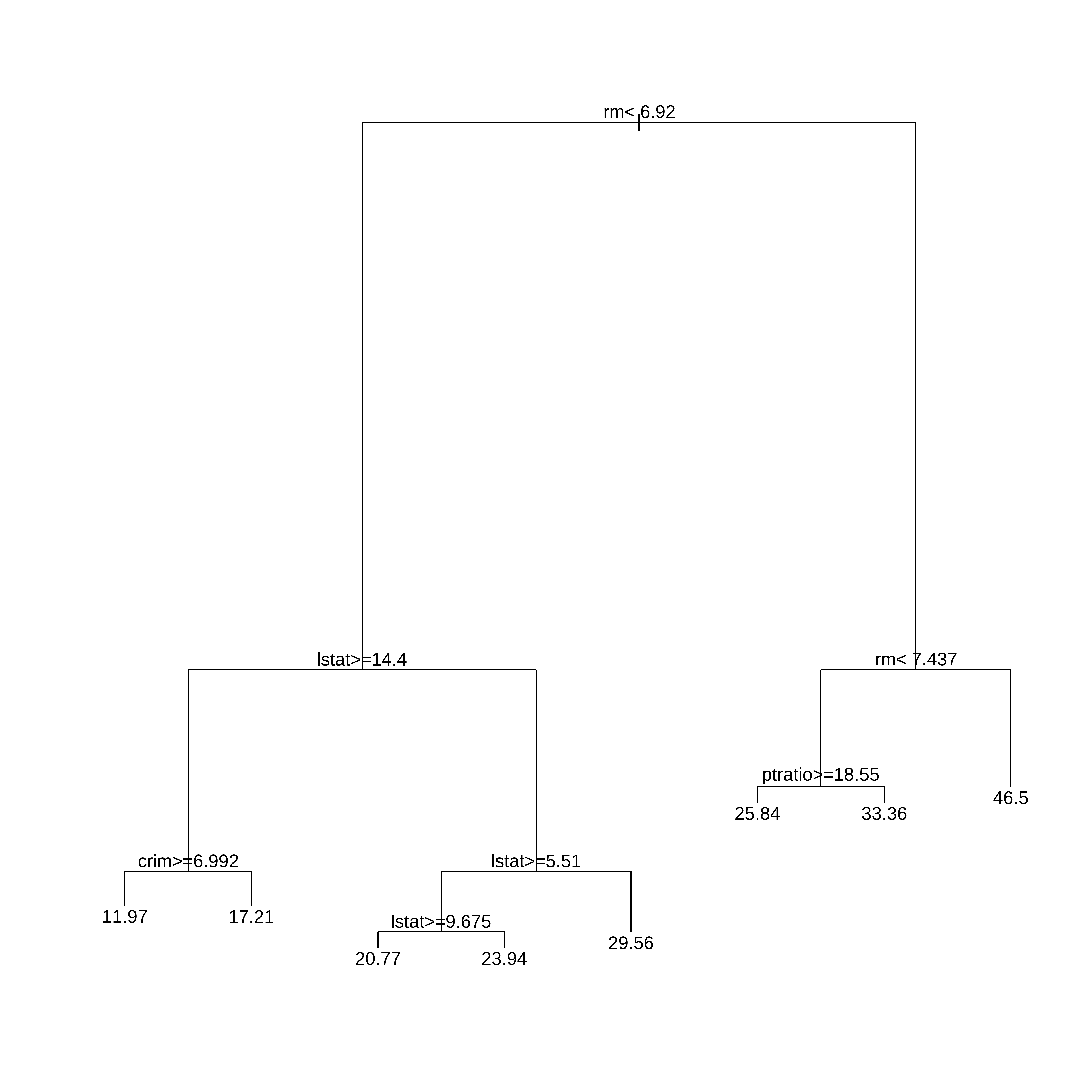

Esta é a principal fragilidade da árvore (única), qualquer mudança na amostra pode trazer uma configuração diferente. ## Fim