Arvores de Classificação - XGboost
Bibliotecas
Dados
Vamos começar a aplicar a metodologia de árvores usando árvores de classificação para analisar os dados existentes em Carseats. Este conjunto de dados (simulado) é sobre venda de assentos de criança para carros. Ele tem 400 observações das seguintes variáveis (11), cujos nomes serão convertidos para o português:
Sales: vendas em unidades (em mil) em cada local
CompPrice: preço cobrado pelo competidor em cada local
Income: nível de renda da comunidade local (em mil US$)
Advertising: orçamento local de propaganda (em mil US$)
Population: população na região (em mil)
Price: preço cobrado pela empresa em cada local
ShelveLoc: um fator com níveis Ruim, Bom e Medio indicando a qualidade da localização das prateleiras para os assentos em cada lugar
Age: idade media da população local
Education: nível de educação em cada local
Urban: um fator Sim e Não indicando se a loja esta em uma área urbana ou rural
US: um fator indicando se a loja é nos EUA ou não
Neste dados, Sales é a variável resposta, só que ela é uma variável contínua, por este motivo vamos usá-la para criar uma variável binária. Vamos usar a função ifelse() para criar a variável binária, que chamaremos de alta, ela assume os valores Sim se Sales for maior que 8 e assume o valor Não caso contrário:
Sales CompPrice Income Advertising
Min. : 0.000 Min. : 77 Min. : 21.00 Min. : 0.000
1st Qu.: 5.390 1st Qu.:115 1st Qu.: 42.75 1st Qu.: 0.000
Median : 7.490 Median :125 Median : 69.00 Median : 5.000
Mean : 7.496 Mean :125 Mean : 68.66 Mean : 6.635
3rd Qu.: 9.320 3rd Qu.:135 3rd Qu.: 91.00 3rd Qu.:12.000
Max. :16.270 Max. :175 Max. :120.00 Max. :29.000
Population Price ShelveLoc Age Education
Min. : 10.0 Min. : 24.0 Bad : 96 Min. :25.00 Min. :10.0
1st Qu.:139.0 1st Qu.:100.0 Good : 85 1st Qu.:39.75 1st Qu.:12.0
Median :272.0 Median :117.0 Medium:219 Median :54.50 Median :14.0
Mean :264.8 Mean :115.8 Mean :53.32 Mean :13.9
3rd Qu.:398.5 3rd Qu.:131.0 3rd Qu.:66.00 3rd Qu.:16.0
Max. :509.0 Max. :191.0 Max. :80.00 Max. :18.0
Urban US
No :118 No :142
Yes:282 Yes:258
str(Carseats)'data.frame': 400 obs. of 11 variables:
$ Sales : num 9.5 11.22 10.06 7.4 4.15 ...
$ CompPrice : num 138 111 113 117 141 124 115 136 132 132 ...
$ Income : num 73 48 35 100 64 113 105 81 110 113 ...
$ Advertising: num 11 16 10 4 3 13 0 15 0 0 ...
$ Population : num 276 260 269 466 340 501 45 425 108 131 ...
$ Price : num 120 83 80 97 128 72 108 120 124 124 ...
$ ShelveLoc : Factor w/ 3 levels "Bad","Good","Medium": 1 2 3 3 1 1 3 2 3 3 ...
$ Age : num 42 65 59 55 38 78 71 67 76 76 ...
$ Education : num 17 10 12 14 13 16 15 10 10 17 ...
$ Urban : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 1 2 2 1 1 ...
$ US : Factor w/ 2 levels "No","Yes": 2 2 2 2 1 2 1 2 1 2 ...# Manipulando os dados
cad_crianca <- Carseats %>% rename(vendas = Sales,
preco_comp = CompPrice,
renda = Income,
propaganda = Advertising,
populacao = Population,
preco = Price,
local_prat = ShelveLoc,
idade = Age,
educacao = Education,
urbano = Urban,
eua = US)
cad_crianca <- cad_crianca %>% mutate(vendaAlta = ifelse(vendas > 8, 1, 0)) %>% select(-vendas)
# Dividir em treino e teste
set.seed(21)
indice <- createDataPartition(cad_crianca$vendaAlta, p = 0.7, list = FALSE)
conj_treino <- cad_crianca[indice, ]
conj_teste <- cad_crianca[-indice, ]
# Codificação dummy para variáveis categóricas
dummies <- dummyVars(vendaAlta ~ ., data = conj_treino)
X_treino <- predict(dummies, newdata = conj_treino)
head(X_treino) preco_comp renda propaganda populacao preco local_prat.Bad local_prat.Good
1 138 73 11 276 120 1 0
3 113 35 10 269 80 0 0
4 117 100 4 466 97 0 0
5 141 64 3 340 128 1 0
7 115 105 0 45 108 0 0
8 136 81 15 425 120 0 1
local_prat.Medium idade educacao urbano.No urbano.Yes eua.No eua.Yes
1 0 42 17 0 1 0 1
3 1 59 12 0 1 0 1
4 1 55 14 0 1 0 1
5 0 38 13 0 1 1 0
7 1 71 15 0 1 1 0
8 0 67 10 0 1 0 1X_teste <- predict(dummies, newdata = conj_teste)
# Criar matrizes DMatrix
dtreino <- xgb.DMatrix(data = X_treino, label = conj_treino$vendaAlta)
dteste <- xgb.DMatrix(data = X_teste, label = conj_teste$vendaAlta)# Previsões
pred_prob <- predict(model, dteste)
pred_class <- ifelse(pred_prob > 0.5, 1, 0)
# Matriz de confusão
conf_matrix <- confusionMatrix(factor(pred_class), factor(conj_teste$vendaAlta), positive = "1")
conf_matrixConfusion Matrix and Statistics
Reference
Prediction 0 1
0 56 14
1 12 38
Accuracy : 0.7833
95% CI : (0.6989, 0.8533)
No Information Rate : 0.5667
P-Value [Acc > NIR] : 5.495e-07
Kappa : 0.5568
Mcnemar's Test P-Value : 0.8445
Sensitivity : 0.7308
Specificity : 0.8235
Pos Pred Value : 0.7600
Neg Pred Value : 0.8000
Prevalence : 0.4333
Detection Rate : 0.3167
Detection Prevalence : 0.4167
Balanced Accuracy : 0.7771
'Positive' Class : 1
roc_obj <- roc(conj_teste$vendaAlta, pred_prob)
plot(roc_obj, main = "Curva ROC - XGBoost", col = "blue")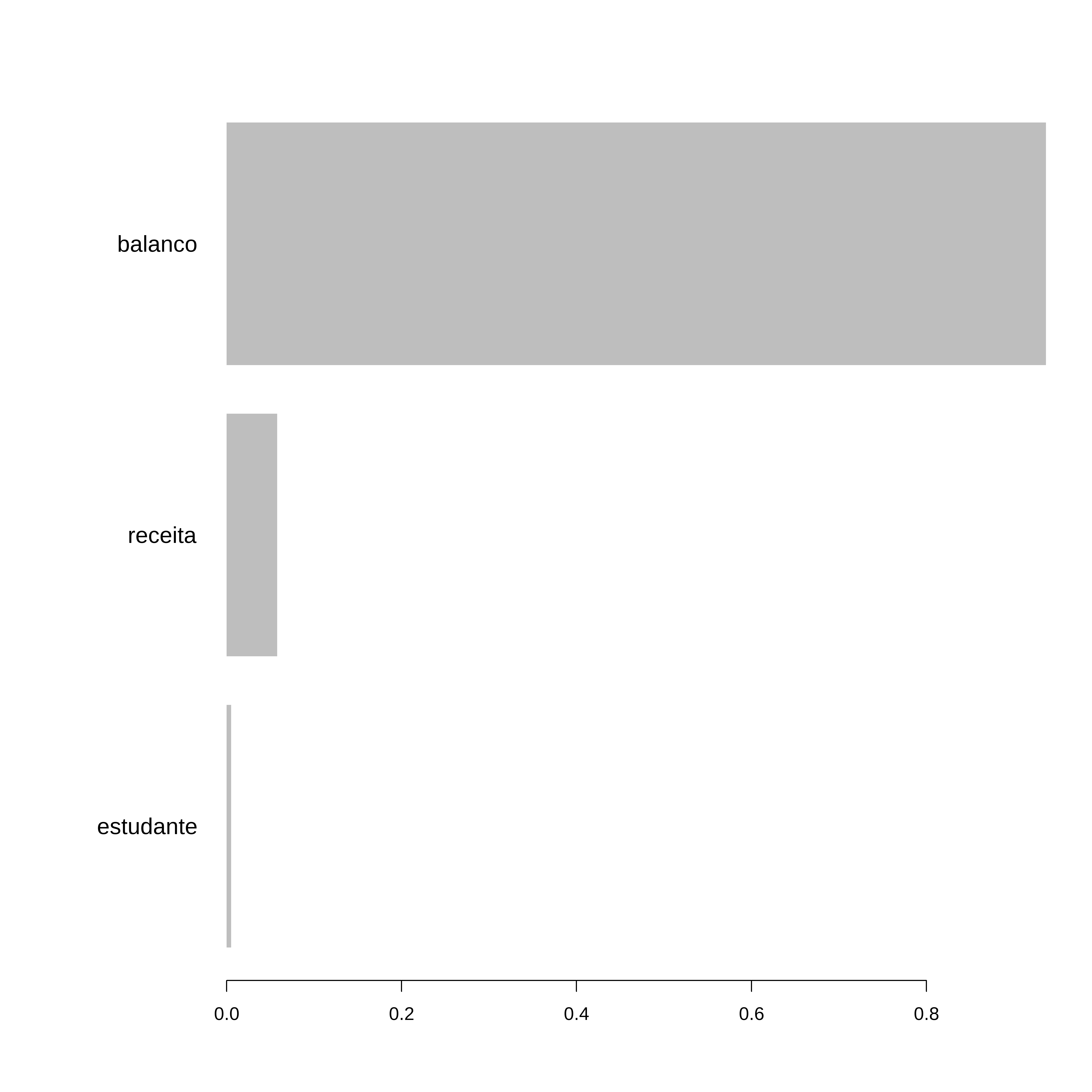
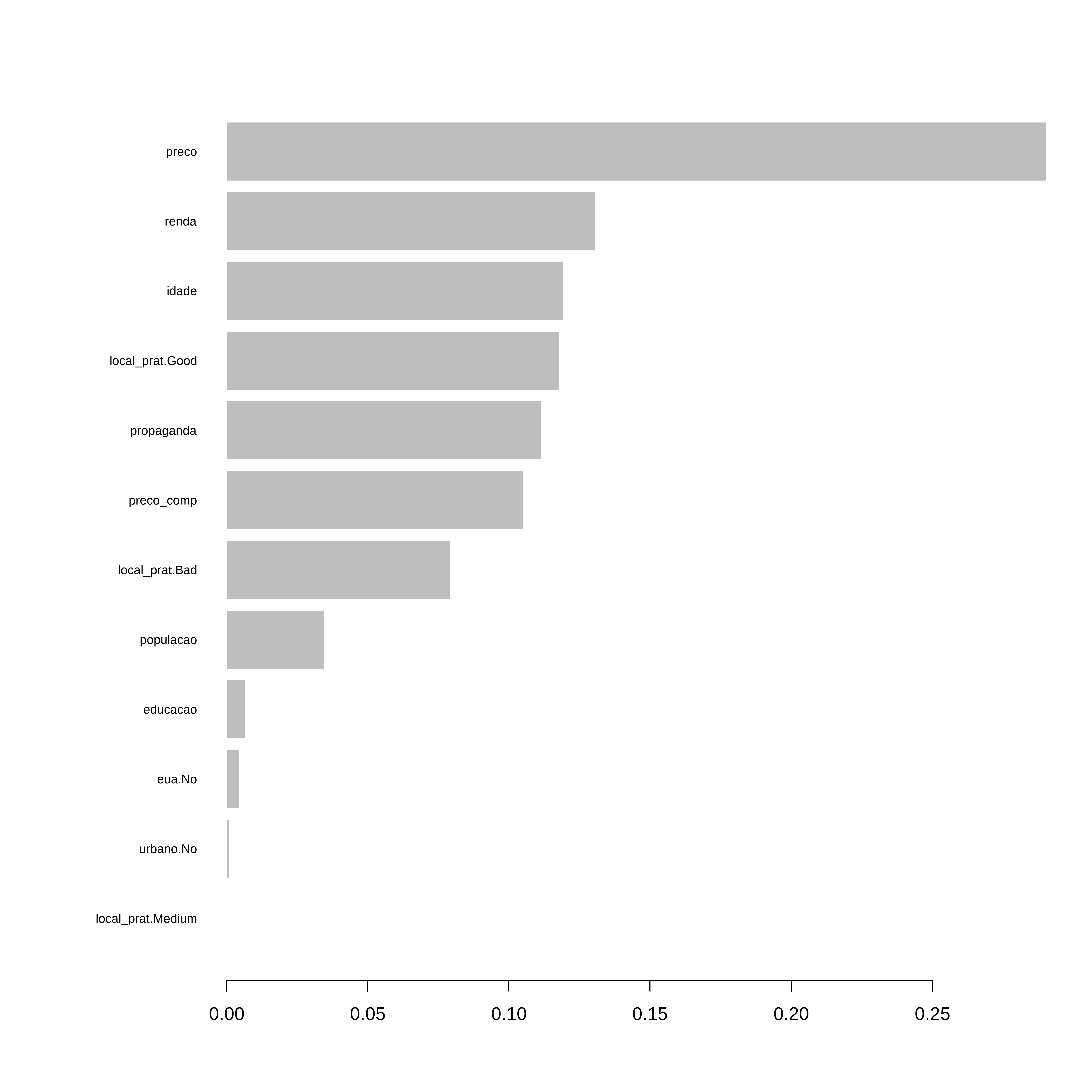
auc(roc_obj)Area under the curve: 0.8767importance <- xgb.importance(model = model)
xgb.plot.importance(importance_matrix = importance)