Arvores de Classificação - Única e GBM

Carregando Bibliotecas

library(tidyverse)
library(ISLR)
data(Default)
summary(Default)

 default    student       balance           income     
 No :9667   No :7056   Min.   :   0.0   Min.   :  772  
 Yes: 333   Yes:2944   1st Qu.: 481.7   1st Qu.:21340  
                       Median : 823.6   Median :34553  
                       Mean   : 835.4   Mean   :33517  
                       3rd Qu.:1166.3   3rd Qu.:43808  
                       Max.   :2654.3   Max.   :73554  

str(Default)

'data.frame':   10000 obs. of  4 variables:
 $ default: Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 ...
 $ student: Factor w/ 2 levels "No","Yes": 1 2 1 1 1 2 1 2 1 1 ...
 $ balance: num  730 817 1074 529 786 ...
 $ income : num  44362 12106 31767 35704 38463 ...

head(Default)

  default student   balance    income
1      No      No  729.5265 44361.625
2      No     Yes  817.1804 12106.135
3      No      No 1073.5492 31767.139
4      No      No  529.2506 35704.494
5      No      No  785.6559 38463.496
6      No     Yes  919.5885  7491.559

Manipulando os dados

credito <- tibble(Default)
summary(credito)

 default    student       balance           income     
 No :9667   No :7056   Min.   :   0.0   Min.   :  772  
 Yes: 333   Yes:2944   1st Qu.: 481.7   1st Qu.:21340  
                       Median : 823.6   Median :34553  
                       Mean   : 835.4   Mean   :33517  
                       3rd Qu.:1166.3   3rd Qu.:43808  
                       Max.   :2654.3   Max.   :73554  

# renomeando colunas
credito <- credito %>% 
                rename( inadimplente = default, estudante = student, balanco = balance,
                receita = income)
credito <- credito %>% mutate( inadimplente =  case_when(
                           inadimplente == "No"  ~ "Nao",
                           inadimplente == "Yes" ~ "Sim"
                          )) %>% mutate(inadimplente = factor(inadimplente))
credito <- credito %>% mutate( estudante =  case_when(
                           estudante == "No"  ~ 0,
                           estudante == "Yes" ~ 1
                          )) 

str(credito)

tibble [10,000 × 4] (S3: tbl_df/tbl/data.frame)
 $ inadimplente: Factor w/ 2 levels "Nao","Sim": 1 1 1 1 1 1 1 1 1 1 ...
 $ estudante   : num [1:10000] 0 1 0 0 0 1 0 1 0 0 ...
 $ balanco     : num [1:10000] 730 817 1074 529 786 ...
 $ receita     : num [1:10000] 44362 12106 31767 35704 38463 ...

summary(credito)

 inadimplente   estudante         balanco          receita     
 Nao:9667     Min.   :0.0000   Min.   :   0.0   Min.   :  772  
 Sim: 333     1st Qu.:0.0000   1st Qu.: 481.7   1st Qu.:21340  
              Median :0.0000   Median : 823.6   Median :34553  
              Mean   :0.2944   Mean   : 835.4   Mean   :33517  
              3rd Qu.:1.0000   3rd Qu.:1166.3   3rd Qu.:43808  
              Max.   :1.0000   Max.   :2654.3   Max.   :73554  

Treino e Teste

library(caret)
set.seed(21)
y <- credito$inadimplente
indice_teste <- createDataPartition(y, times = 1, p = 0.2, list = FALSE)

conj_treino <- credito %>% slice(-indice_teste)
conj_teste <- credito %>% slice(indice_teste)

summary(conj_treino)

 inadimplente   estudante         balanco          receita     
 Nao:7733     Min.   :0.0000   Min.   :   0.0   Min.   :  772  
 Sim: 266     1st Qu.:0.0000   1st Qu.: 481.3   1st Qu.:21339  
              Median :0.0000   Median : 819.1   Median :34541  
              Mean   :0.2953   Mean   : 832.7   Mean   :33541  
              3rd Qu.:1.0000   3rd Qu.:1167.1   3rd Qu.:43840  
              Max.   :1.0000   Max.   :2654.3   Max.   :73554  

summary(conj_teste)

 inadimplente   estudante         balanco          receita     
 Nao:1934     Min.   :0.0000   Min.   :   0.0   Min.   : 4755  
 Sim:  67     1st Qu.:0.0000   1st Qu.: 483.5   1st Qu.:21371  
              Median :0.0000   Median : 836.6   Median :34591  
              Mean   :0.2909   Mean   : 846.2   Mean   :33423  
              3rd Qu.:1.0000   3rd Qu.:1163.1   3rd Qu.:43646  
              Max.   :1.0000   Max.   :2461.5   Max.   :71239  

Arvore de Classificação

Na biblioteca rpart as arvores de classificação são obtidas usando o método class. Existem alguns controles que podem ser feitos nos parametros da arvore.

Neste exemplo só definimos o menor conjunto de dados numa partição (minsplit) e o parametro de complexidade cp. Posteriormente vamos ampliar este controle. Um valor de cp muito pequeno ocasiona overfitting e um valor muito grande resulta numa arvore muito pequena (underfitting). Nos dois casos se diminui o desempenho do modelo.

##Usando rpart para desenvolver a arvore  
library(rpart)
arvcl <- rpart(inadimplente ~ ., 
                data=conj_treino,
                method="class", #para arvore de classificação
                control=rpart.control(minsplit=30,cp=0.02))
plot(arvcl)
text(arvcl,pretty=0)

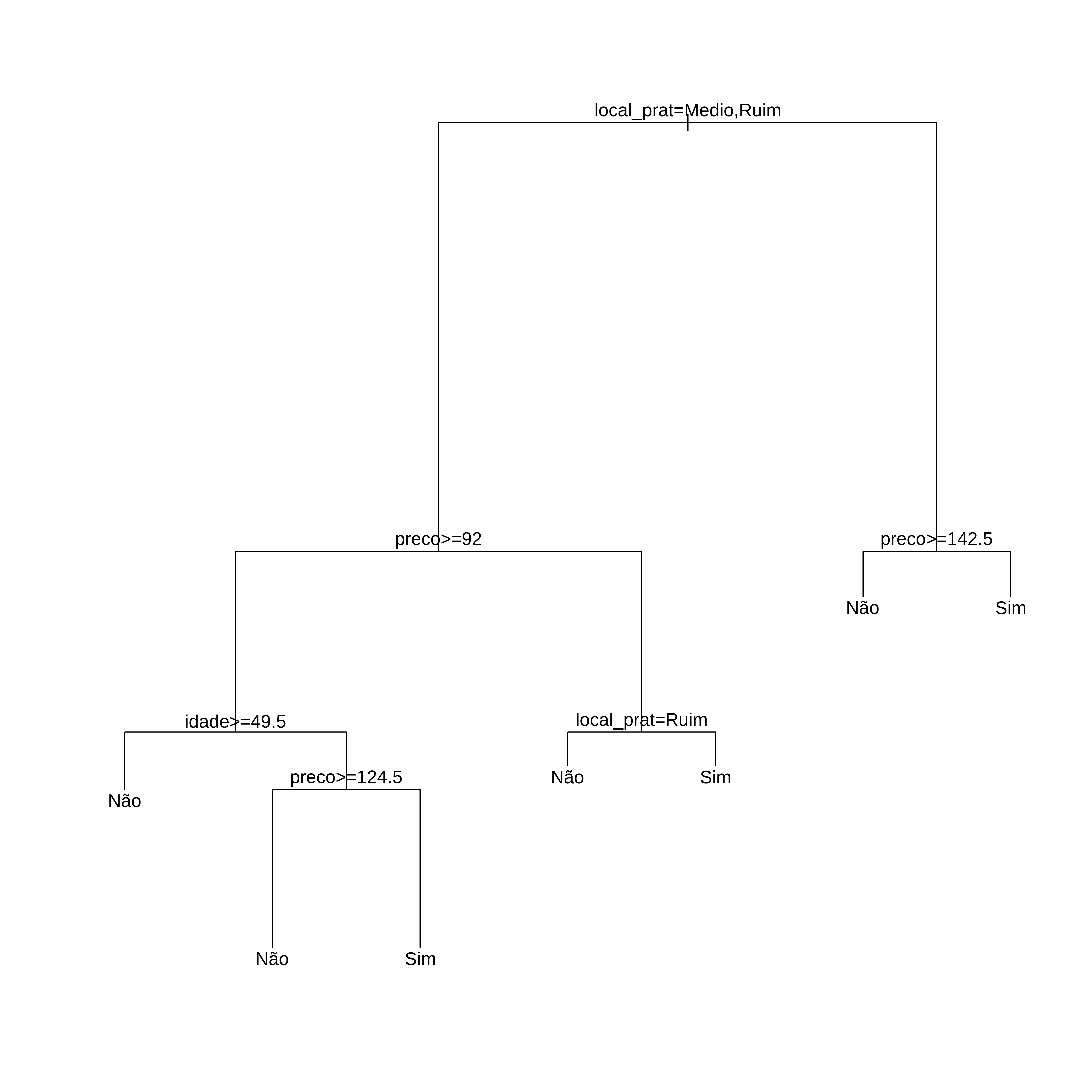
Regras

# Regras de Decisão
arvcl

n= 7999 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

 1) root 7999 266 Nao (0.96674584 0.03325416)  
   2) balanco< 1788.349 7761 136 Nao (0.98247648 0.01752352) *
   3) balanco>=1788.349 238 108 Sim (0.45378151 0.54621849)  
     6) balanco< 1971.915 150  63 Nao (0.58000000 0.42000000)  
      12) receita< 33211.76 105  36 Nao (0.65714286 0.34285714) *
      13) receita>=33211.76 45  18 Sim (0.40000000 0.60000000) *
     7) balanco>=1971.915 88  21 Sim (0.23863636 0.76136364) *

Desenhando a Árvore de uma forma mais clara

library(rattle)
library(rpart.plot)
library(RColorBrewer)
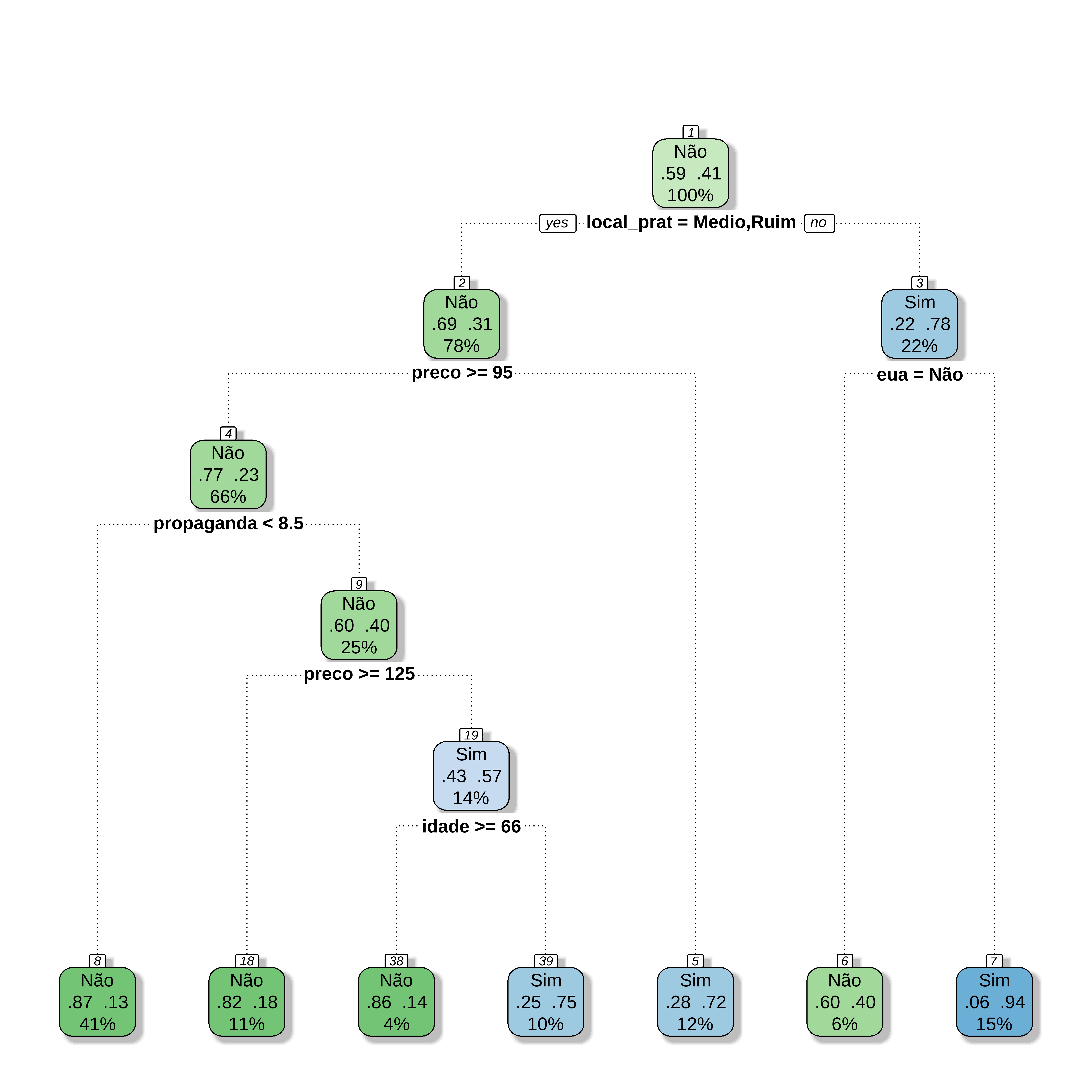
fancyRpartPlot(arvcl, caption = NULL)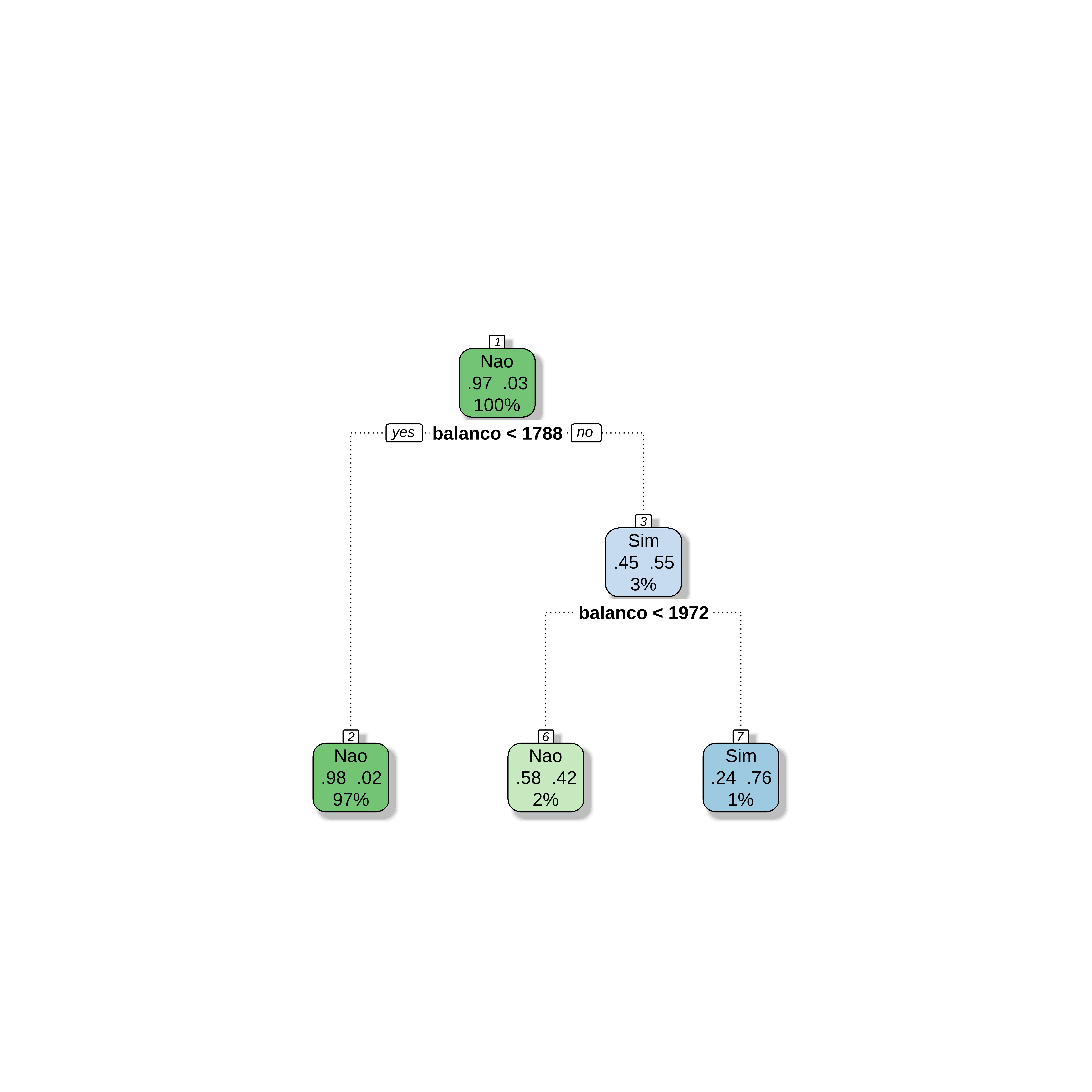

Previsões

# Fazendo Previsões
y_chapeu <- predict(arvcl, newdata = conj_teste, type="class")

confusionMatrix(y_chapeu, conj_teste$inadimplente, positive="Sim") 

Confusion Matrix and Statistics

          Reference
Prediction  Nao  Sim
       Nao 1922   36
       Sim   12   31
                                          
               Accuracy : 0.976           
                 95% CI : (0.9683, 0.9823)
    No Information Rate : 0.9665          
    P-Value [Acc > NIR] : 0.0083176       
                                          
                  Kappa : 0.5519          
                                          
 Mcnemar's Test P-Value : 0.0009009       
                                          
            Sensitivity : 0.46269         
            Specificity : 0.99380         
         Pos Pred Value : 0.72093         
         Neg Pred Value : 0.98161         
             Prevalence : 0.03348         
         Detection Rate : 0.01549         
   Detection Prevalence : 0.02149         
      Balanced Accuracy : 0.72824         
                                          
       'Positive' Class : Sim             
                                          

Arvore de Classificação no caret

##Usando rpart para desenvolver a arvore  
library(rpart)
set.seed(21)
## Otimizamos o valor de cp usando um 10-fold cv
# O parametro tuneLength diz para o algoritmo escolher diferentes valores para cp
# O parametro tuneGrid permite decidir que valores cp deve assumir enquanto que o
# tuneLength somente limita o número default de parametros que se usa.
tgrid <- expand.grid(cp = seq(0.01,0.10,0.001))
ctrl <- trainControl(method = "cv", classProbs=TRUE)
arvclass <- train(inadimplente ~ . , data = conj_treino, method = "rpart",
                 trControl = ctrl,
                 tuneGrid = tgrid
                 )
# Mostra a acurácia vs cp (parametro de complexidade)
plot(arvclass)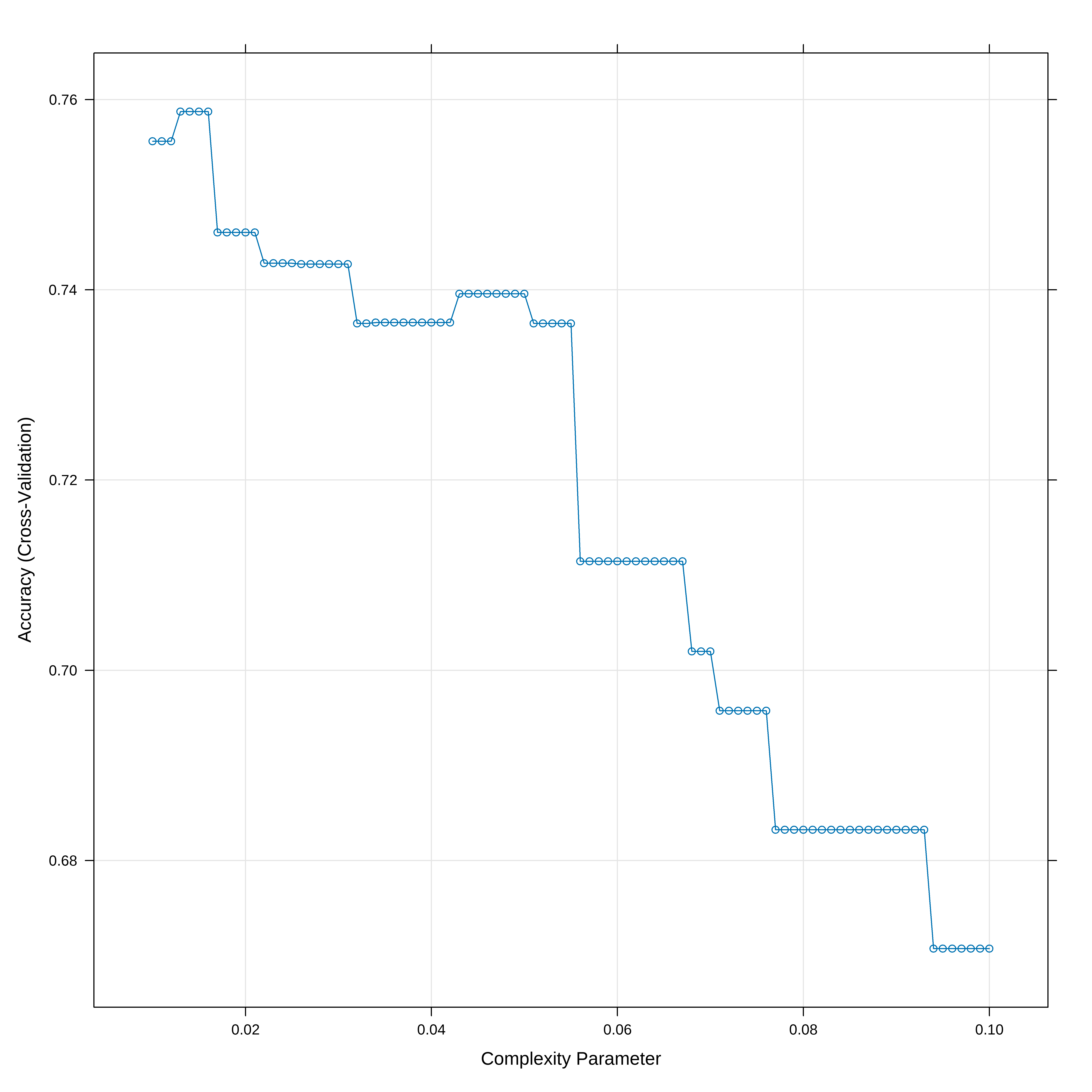

## Indica o melhor valor de cp
arvclass$bestTune

      cp
53 0.062

Uma forma melhor de ver a Árvore

## melhorando apresentação da árvore
library(rattle)
library(rpart.plot)
library(RColorBrewer)
fancyRpartPlot(arvclass$finalModel, caption = NULL)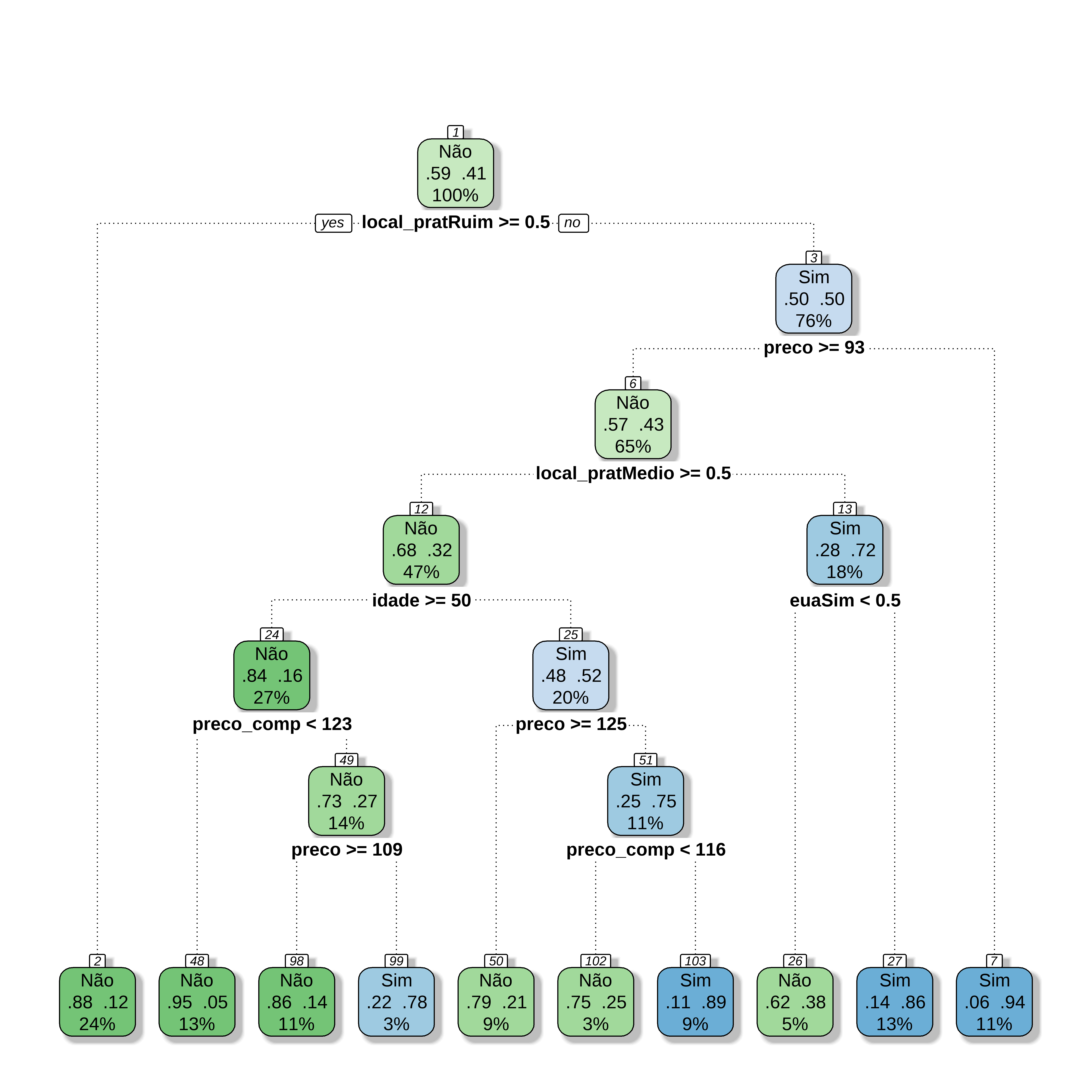

Previsões

# Fazendo Previsões
y_chapeu <- arvclass %>% predict(conj_teste) %>% 
                   factor(levels = levels(conj_teste$inadimplente))
head(y_chapeu)

[1] Nao Nao Nao Nao Nao Nao
Levels: Nao Sim

confusionMatrix(y_chapeu, conj_teste$inadimplente, positive="Sim") 

Confusion Matrix and Statistics

          Reference
Prediction  Nao  Sim
       Nao 1927   44
       Sim    7   23
                                         
               Accuracy : 0.9745         
                 95% CI : (0.9666, 0.981)
    No Information Rate : 0.9665         
    P-Value [Acc > NIR] : 0.02354        
                                         
                  Kappa : 0.4631         
                                         
 Mcnemar's Test P-Value : 4.631e-07      
                                         
            Sensitivity : 0.34328        
            Specificity : 0.99638        
         Pos Pred Value : 0.76667        
         Neg Pred Value : 0.97768        
             Prevalence : 0.03348        
         Detection Rate : 0.01149        
   Detection Prevalence : 0.01499        
      Balanced Accuracy : 0.66983        
                                         
       'Positive' Class : Sim            
                                         

Verificando a consistencia dos resultados

set.seed(121)
y <- credito$inadimplente
indice_teste <- createDataPartition(y, times = 1, p = 0.2, list = FALSE)

conj_treino <- credito %>% slice(-indice_teste)
conj_teste <- credito %>% slice(indice_teste)

str(conj_treino)

tibble [7,999 × 4] (S3: tbl_df/tbl/data.frame)
 $ inadimplente: Factor w/ 2 levels "Nao","Sim": 1 1 1 1 1 1 1 1 1 1 ...
 $ estudante   : num [1:7999] 0 1 0 0 1 0 1 0 1 1 ...
 $ balanco     : num [1:7999] 730 817 1074 786 920 ...
 $ receita     : num [1:7999] 44362 12106 31767 38463 7492 ...

prop.table(table(conj_treino$inadimplente))

       Nao        Sim 
0.96674584 0.03325416 

str(conj_teste)

tibble [2,001 × 4] (S3: tbl_df/tbl/data.frame)
 $ inadimplente: Factor w/ 2 levels "Nao","Sim": 1 1 1 1 1 1 1 1 1 1 ...
 $ estudante   : num [1:2001] 0 0 0 1 0 0 1 1 0 0 ...
 $ balanco     : num [1:2001] 529 1161 1113 1500 1152 ...
 $ receita     : num [1:2001] 35704 37469 23810 13191 42917 ...

prop.table(table(conj_teste$inadimplente))

       Nao        Sim 
0.96651674 0.03348326 

Obtendo a arvore

##Usando rpart para desenvolver a arvore  
library(rpart)
arvcl <- rpart(inadimplente ~ ., 
                data=conj_treino,
                method="class", #para arvore de classificação
                control=rpart.control(minsplit=30,cp=0.02))

Desenhando a Árvore de uma forma mais clara

library(rattle)
library(rpart.plot)
library(RColorBrewer)
fancyRpartPlot(arvcl, caption = NULL)

GBM

Criando um grid para avaliar os parametros

hiper_grid <- expand.grid(
  shrinkage = c(.001, .01, .1),
  interaction.depth = c(1, 3, 5),
  n.minobsinnode = c(5, 10, 15),
  bag.fraction = c(.65, 1),
  optimal_trees = 0, # um lugar para guardar resultados
  min_erro = 0   # um lugar para guardar resultados
  )

# número total de combinações
nrow(hiper_grid)

[1] 54

Avaliando o grid de parametros

library(gbm)
conj_treino$inadimplente <- as.numeric(conj_treino$inadimplente)
conj_treino <- transform(conj_treino, inadimplente=inadimplente - 1)

#Busca no grid
for(i in 1:nrow(hiper_grid)) {

  #
  set.seed(21)

  # treina o modelo
  gbm.tune <- gbm(
    formula = inadimplente ~ .,
    distribution = "bernoulli",
    data = conj_treino,
    n.trees = 2000,
    interaction.depth = hiper_grid$interaction.depth[i],
    shrinkage = hiper_grid$shrinkage[i],
    n.minobsinnode = hiper_grid$n.minobsinnode[i],
    bag.fraction = hiper_grid$bag.fraction[i],
    train.fraction = .75,
    n.cores = NULL,
    verbose = FALSE
  )

  # adiciona os erros de treino e arvores ao grid
  hiper_grid$optimal_trees[i] <- which.min(gbm.tune$valid.error)
  hiper_grid$min_erro[i] <- min(gbm.tune$valid.error)
}

hiper_grid %>% dplyr::arrange(min_erro) %>% head(10)

   shrinkage interaction.depth n.minobsinnode bag.fraction optimal_trees
1       0.10                 1             15         0.65           142
2       0.10                 1             10         0.65           142
3       0.10                 1              5         0.65            84
4       0.10                 1              5         1.00           155
5       0.01                 1              5         1.00          1592
6       0.10                 1             10         1.00           136
7       0.10                 1             15         1.00           136
8       0.01                 1              5         0.65          1002
9       0.01                 1             10         1.00           940
10      0.01                 1             15         1.00           940
    min_erro
1  0.1602066
2  0.1602292
3  0.1604008
4  0.1607106
5  0.1608038
6  0.1611587
7  0.1611587
8  0.1611858
9  0.1612577
10 0.1612577

Modelo final

# 
set.seed(21)

# treina o modelo GBM
gbm.fit.final <- gbm(
  formula = inadimplente ~ .,
  distribution = "bernoulli",
  data = conj_treino,
  n.trees = 193,
  interaction.depth = 1,
  shrinkage = 0.10,
  n.minobsinnode = 5,
  bag.fraction = 1.00, 
  train.fraction = 1,
  n.cores = NULL, 
  verbose = FALSE
  )  

Importância das Variáveis

par(mai = c(1, 2, 1, 2))
summary(
  gbm.fit.final, 
  cBars = 10,
  method = relative.influence, # também pode ser usado permutation.test.gbm
  las = 2
  )

                var    rel.inf
balanco     balanco 99.2361652
estudante estudante  0.4480848
receita     receita  0.3157499

Previsão

conj_teste$inadimplente <- as.numeric(conj_teste$inadimplente)
conj_teste <- transform(conj_teste, inadimplente=inadimplente - 1)

# Fazendo Previsões
previsao1 <- predict(gbm.fit.final, 
                     newdata = conj_teste,
                     n.trees=gbm.fit.final$n.trees,
                     type = "response")
head(previsao1)

[1] 0.002456101 0.015887955 0.013762373 0.099006852 0.015887955 0.002456101

gbm.ychapeu <- as.factor(ifelse(previsao1 < 0.5,0,1))
 
confusionMatrix(gbm.ychapeu,as.factor(conj_teste$inadimplente), positive="1")

Confusion Matrix and Statistics

          Reference
Prediction    0    1
         0 1933   50
         1    1   17
                                         
               Accuracy : 0.9745         
                 95% CI : (0.9666, 0.981)
    No Information Rate : 0.9665         
    P-Value [Acc > NIR] : 0.02354        
                                         
                  Kappa : 0.3914         
                                         
 Mcnemar's Test P-Value : 1.801e-11      
                                         
            Sensitivity : 0.253731       
            Specificity : 0.999483       
         Pos Pred Value : 0.944444       
         Neg Pred Value : 0.974786       
             Prevalence : 0.033483       
         Detection Rate : 0.008496       
   Detection Prevalence : 0.008996       
      Balanced Accuracy : 0.626607       
                                         
       'Positive' Class : 1              
                                         

Curva ROC

library(pROC)
p_chapeu_gbm <- previsao1
roc_gbm <- roc(conj_teste$inadimplente ~ p_chapeu_gbm, plot = TRUE, print.auc=FALSE, col="black", legacy.axes=TRUE)

as.numeric(roc_gbm$auc)

[1] 0.9536804