Arvores de Regressão - Random Forest
Bibliotecas
Avaliando, selecionando dados
Treino e Teste com todas as variáveis
## Vamos criar os conjuntos de treino teste e desenvolver a arvore
## com todas as variáveis.
library(caret)
set.seed(21)
indice <- createDataPartition(dados$medv, times=1, p=0.75, list=FALSE)
conj_treino <- dados[indice,]
conj_teste <- dados[-indice,]
head(conj_treino) crim zn indus chas nox rm age dis rad tax ptratio black lstat
1 0.00632 18.0 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98
3 0.02729 0.0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03
4 0.03237 0.0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94
5 0.06905 0.0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33
6 0.02985 0.0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21
7 0.08829 12.5 7.87 0 0.524 6.012 66.6 5.5605 5 311 15.2 395.60 12.43
medv
1 24.0
3 34.7
4 33.4
5 36.2
6 28.7
7 22.9head(conj_teste) crim zn indus chas nox rm age dis rad tax ptratio black lstat
2 0.02731 0.0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14
10 0.17004 12.5 7.87 0 0.524 6.004 85.9 6.5921 5 311 15.2 386.71 17.10
12 0.11747 12.5 7.87 0 0.524 6.009 82.9 6.2267 5 311 15.2 396.90 13.27
16 0.62739 0.0 8.14 0 0.538 5.834 56.5 4.4986 4 307 21.0 395.62 8.47
19 0.80271 0.0 8.14 0 0.538 5.456 36.6 3.7965 4 307 21.0 288.99 11.69
23 1.23247 0.0 8.14 0 0.538 6.142 91.7 3.9769 4 307 21.0 396.90 18.72
medv
2 21.6
10 18.9
12 18.9
16 19.9
19 20.2
23 15.2Criando um grid de parametros
grid_params <- expand.grid(
mtry = c(2, 4, 6),
min.node.size = c(1, 5),
splitrule = c("variance", "extratrees"),
num.trees = c(100)
)
nrow(grid_params)[1] 12head(grid_params) mtry min.node.size splitrule num.trees
1 2 1 variance 100
2 4 1 variance 100
3 6 1 variance 100
4 2 5 variance 100
5 4 5 variance 100
6 6 5 variance 100Validação cruzada com rsample
Ajuste do modelo Random Forest com cada combinação
avaliacoes <- grid_params %>%
mutate(
media_rmse = pmap_dbl(list(mtry, min.node.size, splitrule, num.trees),
function(mtry, min.node.size, splitrule, num.trees) {
rmse_fold <- map_dbl(folds$splits, function(split) {
treino <- analysis(split)
teste <- assessment(split)
modelo <- ranger(
medv ~ .,
data = treino,
mtry = mtry,
min.node.size = min.node.size,
splitrule = splitrule,
num.trees = num.trees,
seed = 123
)
pred <- predict(modelo, data = teste)$predictions
metric <- yardstick::rmse_vec(truth = teste$medv, estimate = pred)
return(metric)
})
mean(rmse_fold)
}
)
)
avaliacoes %>% arrange(media_rmse) %>% head() mtry min.node.size splitrule num.trees media_rmse
1 6 1 variance 100 3.138929
2 6 5 variance 100 3.180183
3 4 1 variance 100 3.182037
4 6 1 extratrees 100 3.223310
5 4 5 variance 100 3.223342
6 6 5 extratrees 100 3.292367Melhor combinação de parâmetros
Ajuste do modelo final
modelo_final <- ranger(
medv ~ .,
data = conj_treino,
mtry = melhor_param$mtry,
min.node.size = melhor_param$min.node.size,
splitrule = melhor_param$splitrule,
num.trees = melhor_param$num.trees,
seed = 2025,
importance = "permutation"
)
modelo_finalRanger result
Call:
ranger(medv ~ ., data = conj_treino, mtry = melhor_param$mtry, min.node.size = melhor_param$min.node.size, splitrule = melhor_param$splitrule, num.trees = melhor_param$num.trees, seed = 2025, importance = "permutation")
Type: Regression
Number of trees: 100
Sample size: 381
Number of independent variables: 13
Mtry: 6
Target node size: 1
Variable importance mode: permutation
Splitrule: 1
OOB prediction error (MSE): 12.75977
R squared (OOB): 0.8445772 Avaliação no conjunto de teste
pred <- predict(modelo_final, data = conj_teste)$predictions
# Métricas de desempenho
postResample(pred, conj_teste$medv) RMSE Rsquared MAE
4.0052763 0.8341371 2.2677500 Importância das variáveis
# Converter a importância em tibble ordenada
df_importancia <- importance(modelo_final) %>%
enframe(name = "Variável", value = "Importância") %>%
arrange(desc(Importância))
# Gráfico de barras da importância das variáveis
ggplot(df_importancia, aes(x = reorder(Variável, Importância), y = Importância)) +
geom_col(fill = "steelblue") +
coord_flip() +
labs(title = "Importância das Variáveis (Permutação)",
x = "Variável",
y = "Importância") +
theme_minimal()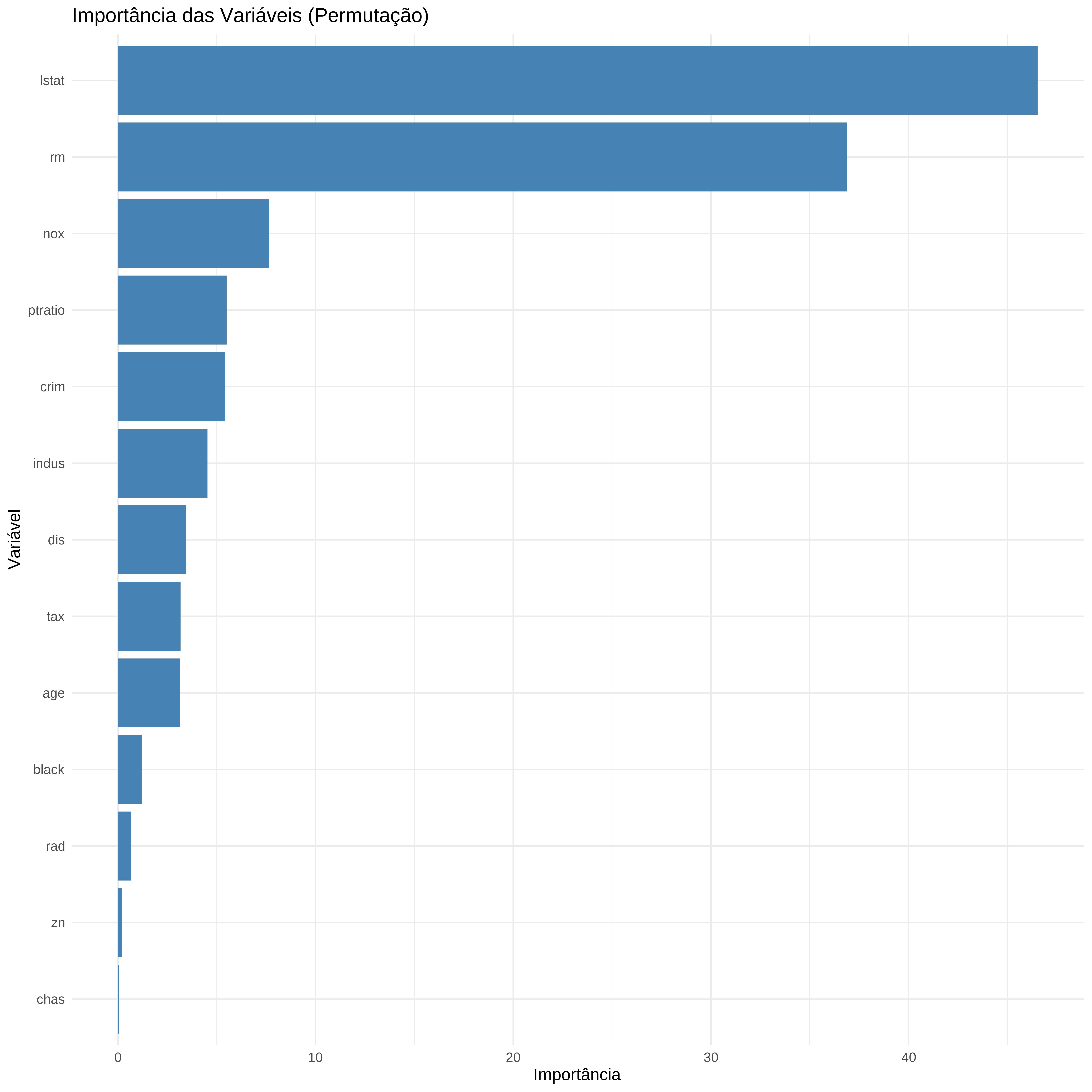
Comparação com outro modelo (Regressão Linear)
ctrl <- trainControl(method = "cv", number = 5)
model_lm <- train(
medv ~ ., data = conj_treino,
method = "lm",
trControl = ctrl
)
pred_lm <- predict(model_lm, newdata = conj_teste)
postResample(pred_lm, conj_teste$medv) RMSE Rsquared MAE
5.9426142 0.6315418 3.9610503 Grafico de comparação
# Gráfico de comparação
graf_comparacao <- ggplot() +
geom_point(aes(x = conj_teste$medv, y = pred), color = "blue", alpha = 0.5) +
geom_point(aes(x = conj_teste$medv, y = pred_lm), color = "red", alpha = 0.5) +
labs(title = "Comparação de Previsões: Random Forest vs Regressão Linear",
x = "Valores Reais (medv)", y = "Previsões") +
theme_minimal()
graf_comparacao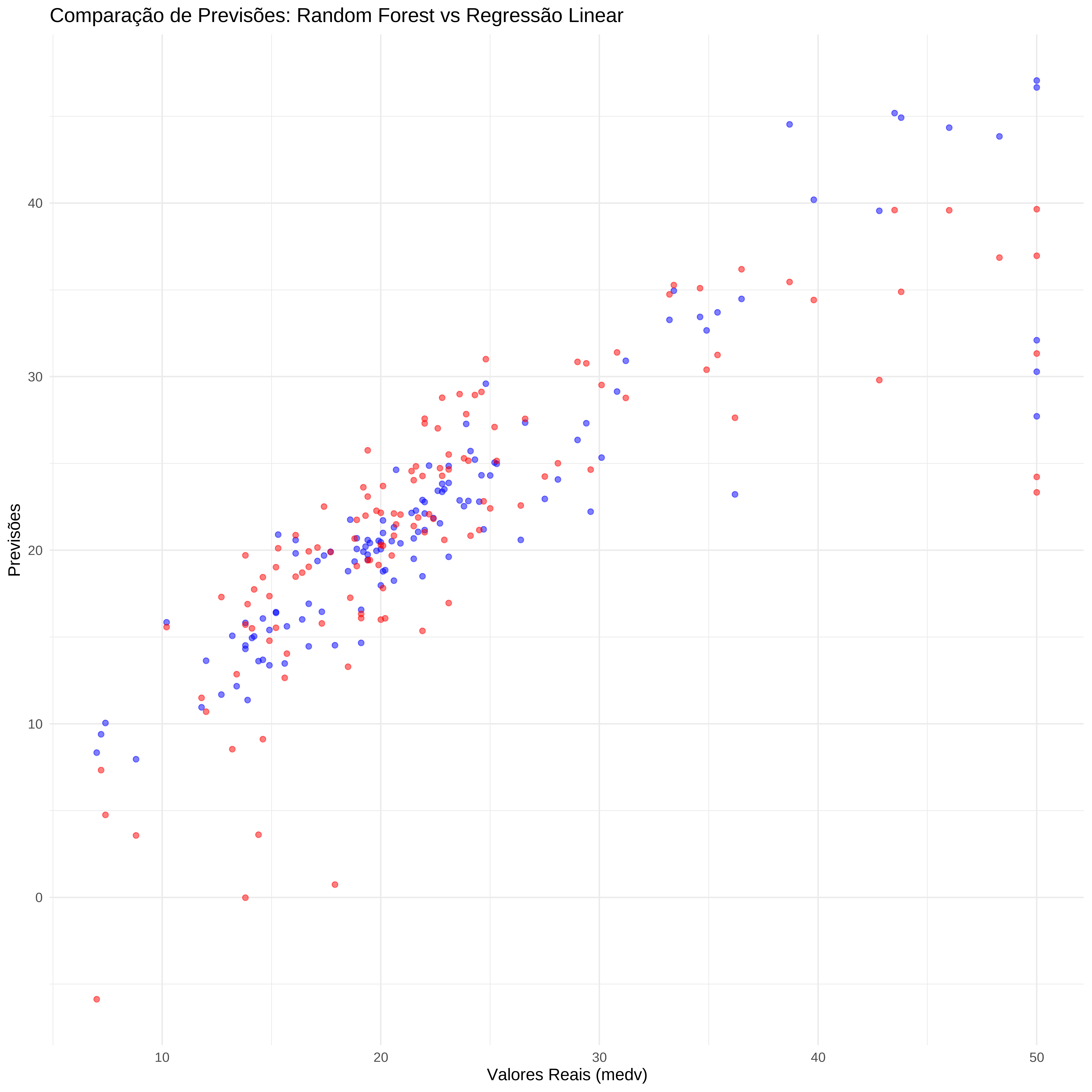
Analisando com o LIME
# Treinamento com ranger precisa ser refeito em formato compatível com lime
library(lime)
# Treinando modelo com train() + ranger para compatibilidade com LIME
set.seed(2025)
tune_grid <- data.frame(
mtry = melhor_param$mtry,
splitrule = as.character(melhor_param$splitrule),
min.node.size = melhor_param$min.node.size
)
modelo_caret <- train(
medv ~ .,
data = conj_treino,
method = "ranger",
trControl = trainControl(method = "none"),
tuneGrid = tune_grid
)
# Preparar explicador LIME
explainer <- lime(conj_treino, modelo_caret, bin_continuous = FALSE)
# Aplicar LIME a 3 observações novas
explicacoes <- explain(
conj_teste[1:3, ],
explainer = explainer,
n_features = 5,
n_labels = 1
)
# Dados Analisados
conj_teste[1:3, c("medv", "rm", "ptratio", "nox", "dis", "lstat", "tax")] medv rm ptratio nox dis lstat tax
2 21.6 6.421 17.8 0.469 4.9671 9.14 242
10 18.9 6.004 15.2 0.524 6.5921 17.10 311
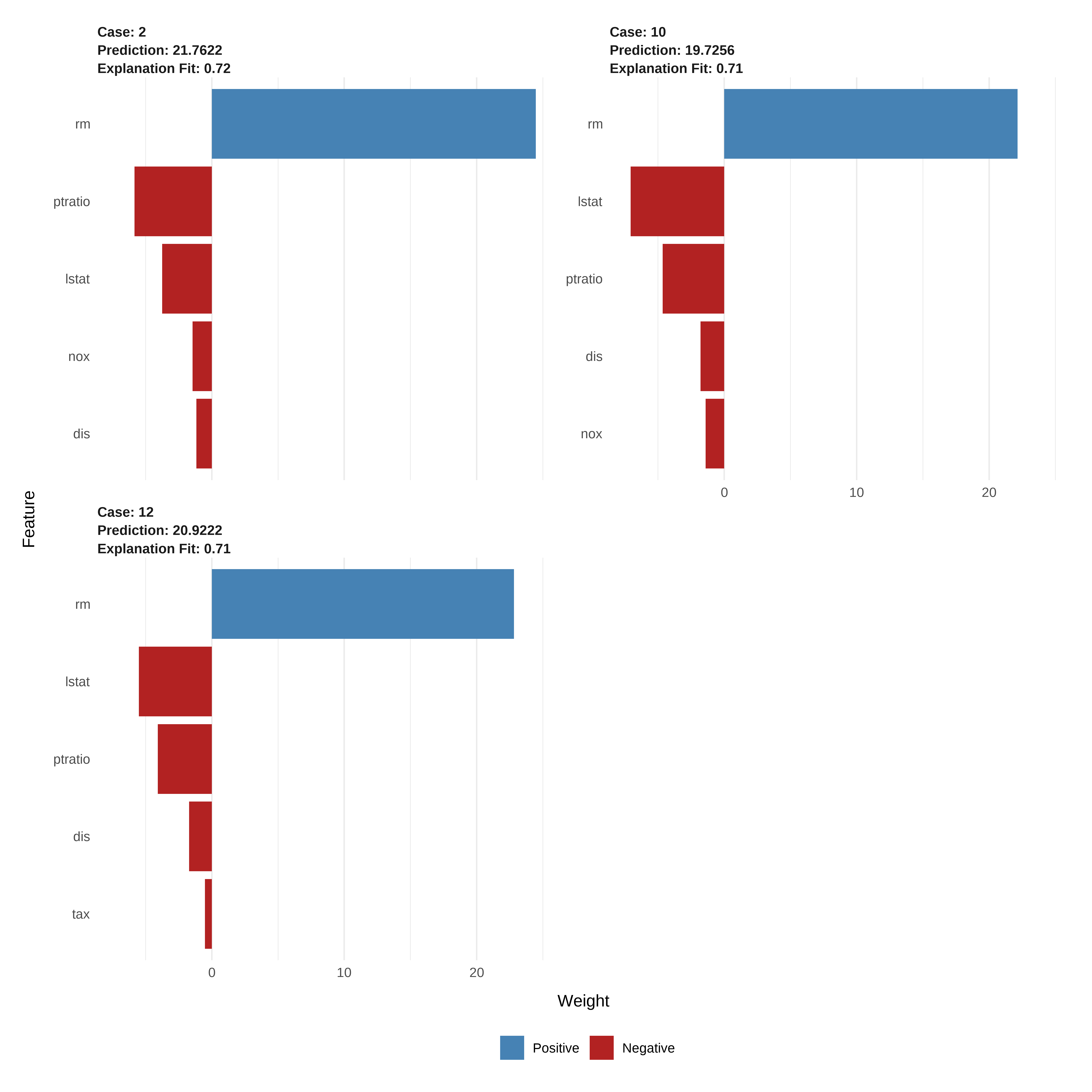
12 18.9 6.009 15.2 0.524 6.2267 13.27 311# Visualizar explicações
plot_features(explicacoes)