#> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr 1.1.4 ✔ readr 2.1.5
#> ✔ forcats 1.0.0 ✔ stringr 1.5.1
#> ✔ ggplot2 3.5.2 ✔ tibble 3.3.0
#> ✔ lubridate 1.9.4 ✔ tidyr 1.3.1
#> ✔ purrr 1.1.0
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsRegressão Linear Múltipla
Carregando bibliotecas
Dados de propaganda
O conjunto de dados contém estatísticas sobre as vendas de um produto em 200 diferentes mercados, juntamente com orçamentos publicitários em cada um desses mercados, para diferentes canais de mídia: TV, rádio e jornal. As vendas estão em milhares de unidades e o orçamento está em milhares de dólares.
library(readxl)
propaganda <- read_excel("Propaganda.xlsx")
summary(propaganda)#> TV Radio Newspaper Sales
#> Min. : 0.70 Min. : 0.000 Min. : 0.30 Min. : 1.60
#> 1st Qu.: 74.38 1st Qu.: 9.975 1st Qu.: 12.75 1st Qu.:10.38
#> Median :149.75 Median :22.900 Median : 25.75 Median :12.90
#> Mean :147.04 Mean :23.264 Mean : 30.55 Mean :14.02
#> 3rd Qu.:218.82 3rd Qu.:36.525 3rd Qu.: 45.10 3rd Qu.:17.40
#> Max. :296.40 Max. :49.600 Max. :114.00 Max. :27.00Renomeando
Sumario
summary(propaganda)#> TV Radio Jornal Vendas
#> Min. : 0.70 Min. : 0.000 Min. : 0.30 Min. : 1.60
#> 1st Qu.: 74.38 1st Qu.: 9.975 1st Qu.: 12.75 1st Qu.:10.38
#> Median :149.75 Median :22.900 Median : 25.75 Median :12.90
#> Mean :147.04 Mean :23.264 Mean : 30.55 Mean :14.02
#> 3rd Qu.:218.82 3rd Qu.:36.525 3rd Qu.: 45.10 3rd Qu.:17.40
#> Max. :296.40 Max. :49.600 Max. :114.00 Max. :27.00nrow(propaganda)#> [1] 200Criando amostra de treino e teste
#> Carregando pacotes exigidos: lattice#>
#> Anexando pacote: 'caret'#> O seguinte objeto é mascarado por 'package:purrr':
#>
#> liftset.seed(21)
y <- propaganda$Vendas
indice_teste <- createDataPartition(y, times = 1, p = 0.40, list = FALSE)
conj_treino <- propaganda[-indice_teste, ]
conj_teste <- propaganda[indice_teste, ]
str(conj_treino)#> tibble [119 × 4] (S3: tbl_df/tbl/data.frame)
#> $ TV : num [1:119] 230.1 151.5 180.8 199.8 66.1 ...
#> $ Radio : num [1:119] 37.8 41.3 10.8 2.6 5.8 35.1 7.6 47.7 20.5 23.9 ...
#> $ Jornal: num [1:119] 69.2 58.5 58.4 21.2 24.2 65.9 7.2 52.9 18.3 19.1 ...
#> $ Vendas: num [1:119] 22.1 18.5 12.9 10.6 8.6 9.2 9.7 22.4 11.3 14.6 ...str(conj_teste)#> tibble [81 × 4] (S3: tbl_df/tbl/data.frame)
#> $ TV : num [1:81] 44.5 17.2 8.7 57.5 120.2 ...
#> $ Radio : num [1:81] 39.3 45.9 48.9 32.8 19.6 2.1 24 32.9 36.6 39.6 ...
#> $ Jornal: num [1:81] 45.1 69.3 75 23.5 11.6 1 4 46 114 55.8 ...
#> $ Vendas: num [1:81] 10.4 9.3 7.2 11.8 13.2 4.8 17.4 19 12.5 24.4 ...| Conjunto de Treino | |||
|---|---|---|---|
| TV | Radio | Jornal | Vendas |
| 230.1 | 37.8 | 69.2 | 22.1 |
| 151.5 | 41.3 | 58.5 | 18.5 |
| 180.8 | 10.8 | 58.4 | 12.9 |
| 199.8 | 2.6 | 21.2 | 10.6 |
| 66.1 | 5.8 | 24.2 | 8.6 |
| 23.8 | 35.1 | 65.9 | 9.2 |
E se eu usar uma outra semente?
set.seed(1234)
y2 <- propaganda$Vendas
indice_teste2 <- createDataPartition(y2, times = 1, p = 0.40, list = FALSE)
conj_treino2 <- propaganda[-indice_teste2, ]
conj_teste2 <- propaganda[indice_teste2, ]
gt(head(conj_treino2, 6)) %>%
tab_header(title = "2o Conjunto de Treino")| 2o Conjunto de Treino | |||
|---|---|---|---|
| TV | Radio | Jornal | Vendas |
| 44.5 | 39.3 | 45.1 | 10.4 |
| 17.2 | 45.9 | 69.3 | 9.3 |
| 151.5 | 41.3 | 58.5 | 18.5 |
| 8.7 | 48.9 | 75.0 | 7.2 |
| 120.2 | 19.6 | 11.6 | 13.2 |
| 8.6 | 2.1 | 1.0 | 4.8 |
library(dlookr)
diagnose_numeric(conj_treino)#> # A tibble: 4 × 10
#> variables min Q1 mean median Q3 max zero minus outlier
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <int> <int>
#> 1 TV 0.7 77.3 151. 150. 225. 294. 0 0 0
#> 2 Radio 0.3 8.3 21.3 20.5 32.6 49.4 0 0 0
#> 3 Jornal 1.8 13.6 29.4 24.2 41 89.4 0 0 1
#> 4 Vendas 1.6 10.4 13.9 12.9 17.2 26.2 0 0 0diagnose_numeric(conj_treino2)#> # A tibble: 4 × 10
#> variables min Q1 mean median Q3 max zero minus outlier
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <int> <int>
#> 1 TV 0.7 67.6 143. 143. 217. 294. 0 0 0
#> 2 Radio 0.4 12.4 24.3 24 36.3 49.6 0 0 0
#> 3 Jornal 0.3 12.5 29.7 26.4 43.8 89.4 0 0 0
#> 4 Vendas 1.6 10.4 14.0 12.8 17.4 27 0 0 0Veja que as amostram ficaram com resultados diferentes, o que levaria a obtermos modelos diferentes num ajuste de regressão!
Regressão Simples
Avaliando as correlações
#> corrplot 0.95 loaded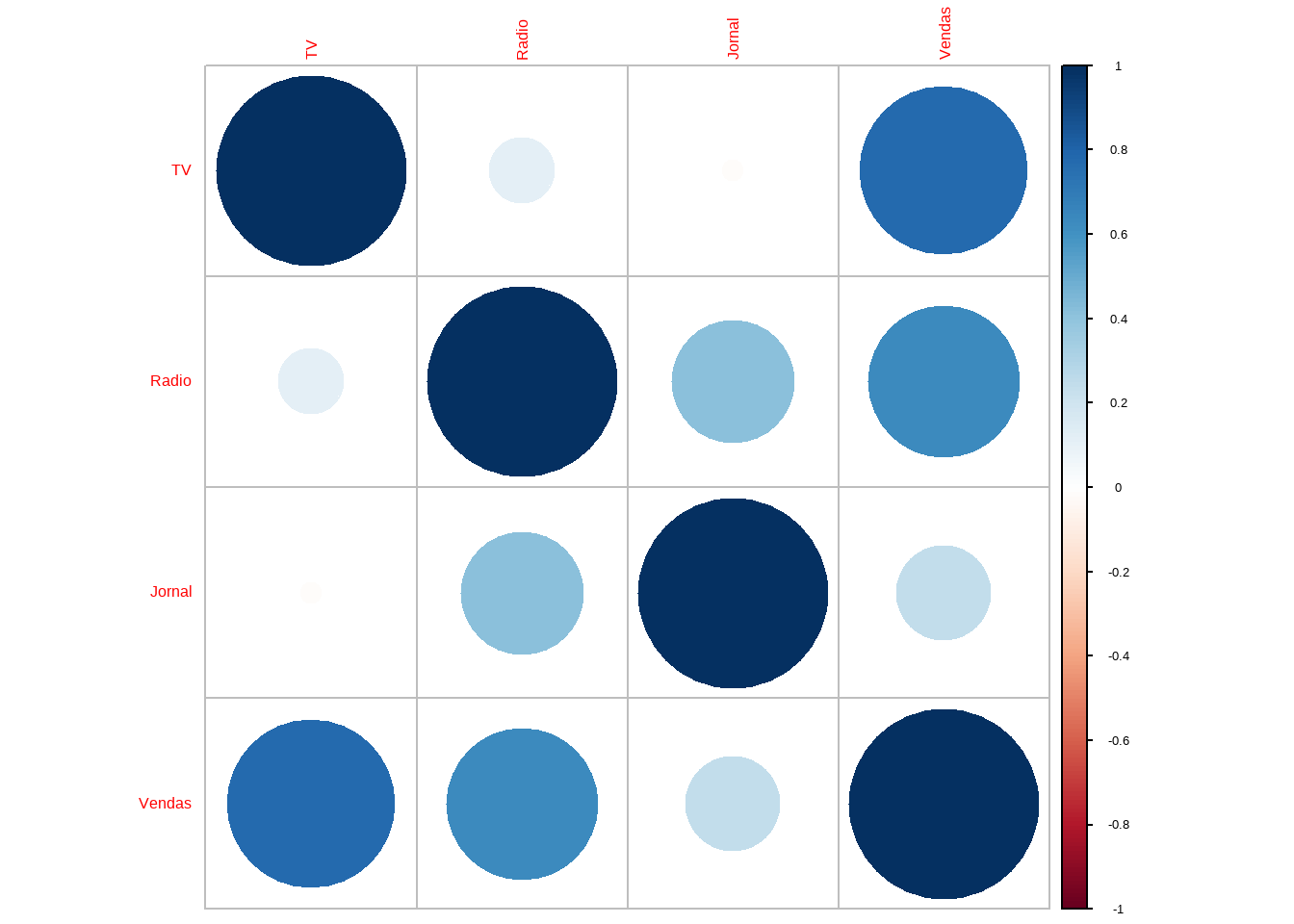
corrplot(mat_corr,method = "number")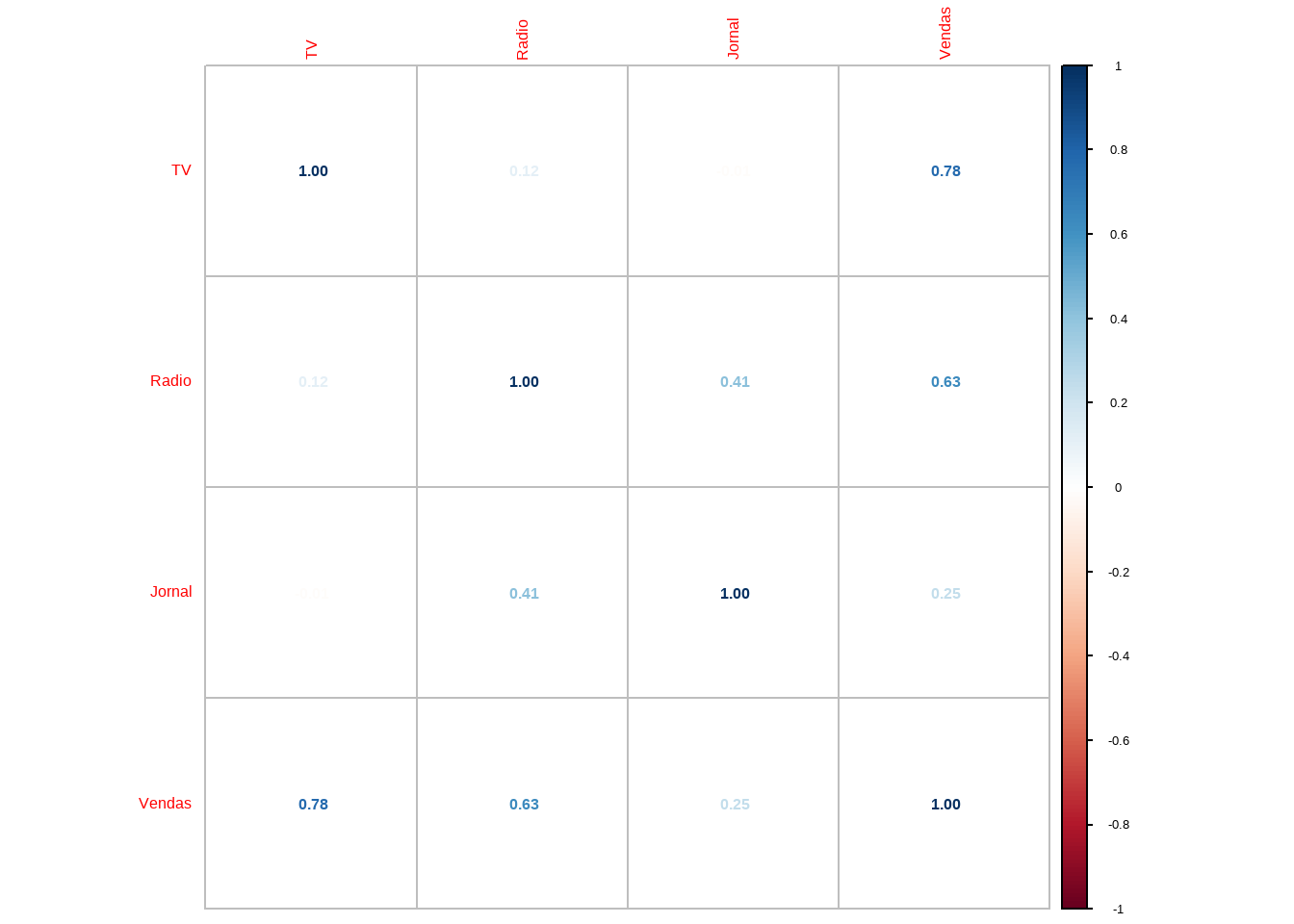
cor(conj_treino)#> TV Radio Jornal Vendas
#> TV 1.00000000 0.1193634 -0.01192443 0.7778348
#> Radio 0.11936345 1.0000000 0.41432470 0.6313682
#> Jornal -0.01192443 0.4143247 1.00000000 0.2466562
#> Vendas 0.77783481 0.6313682 0.24665616 1.00000001a Regressão Multipla
#> Carregando pacotes exigidos: carData#>
#> Anexando pacote: 'car'#> O seguinte objeto é mascarado por 'package:dplyr':
#>
#> recode#> O seguinte objeto é mascarado por 'package:purrr':
#>
#> somescatterplotMatrix(conj_treino)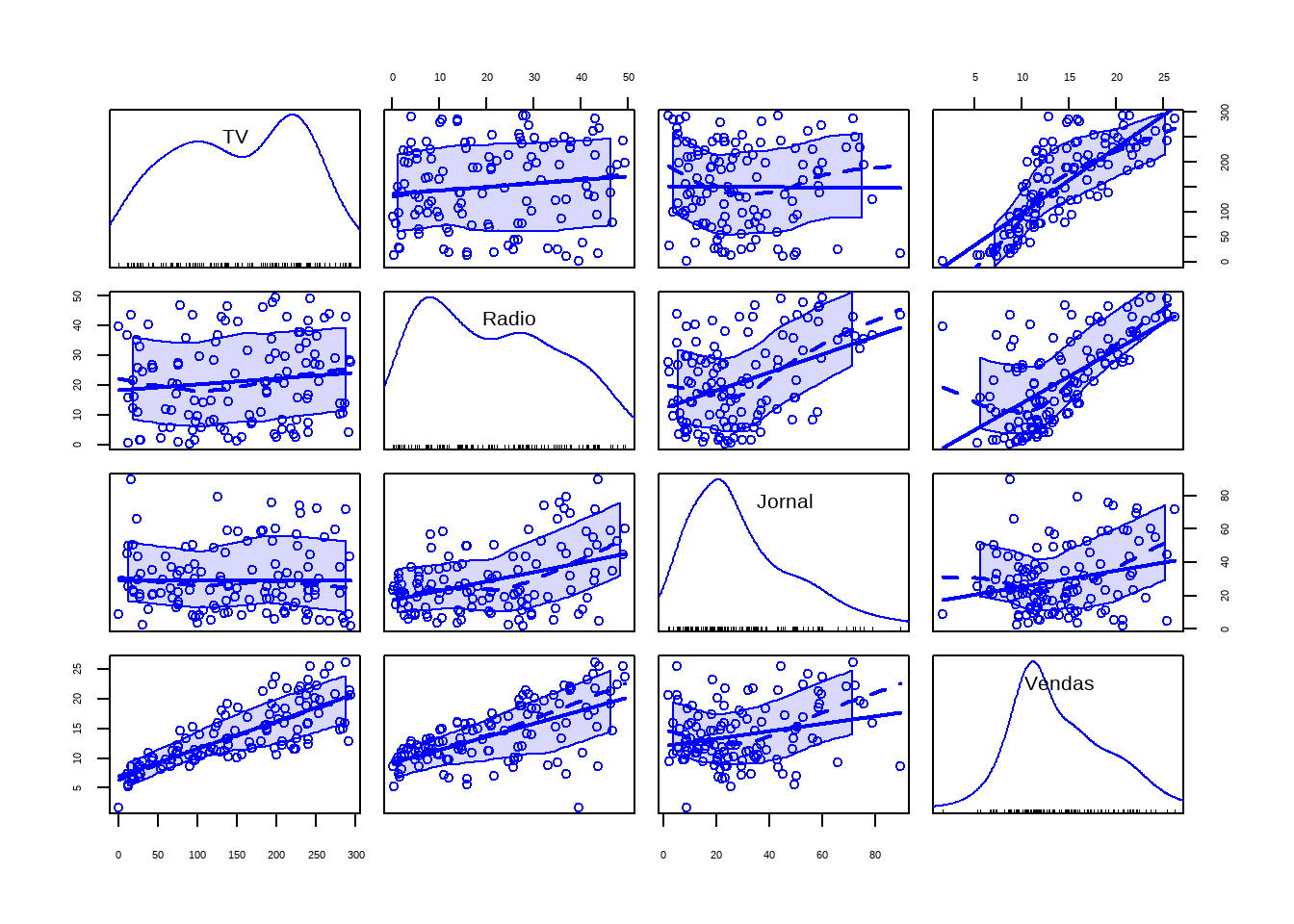
#>
#> Call:
#> lm(formula = Vendas ~ TV + Radio + Jornal, data = conj_treino)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -9.1595 -0.6961 0.2676 1.0298 2.5871
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.268910 0.391828 8.343 1.81e-13 ***
#> TV 0.042705 0.001776 24.039 < 2e-16 ***
#> Radio 0.186439 0.011458 16.272 < 2e-16 ***
#> Jornal 0.008931 0.008292 1.077 0.284
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.606 on 115 degrees of freedom
#> Multiple R-squared: 0.9002, Adjusted R-squared: 0.8976
#> F-statistic: 345.9 on 3 and 115 DF, p-value: < 2.2e-16Vejam que ao analisarmos a estatística t de Jornal percebemos que não podemos rejeitar a hipótese de que o coeficiente de Jornal possa ser zero.
Vamos refazer o modleo sem Jornal.
2a Regressao Multipla
#>
#> Call:
#> lm(formula = Vendas ~ TV + Radio, data = conj_treino)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -9.4585 -0.6886 0.1687 1.0799 2.5529
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.441076 0.357985 9.612 <2e-16 ***
#> TV 0.042575 0.001774 24.005 <2e-16 ***
#> Radio 0.191607 0.010412 18.402 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.607 on 116 degrees of freedom
#> Multiple R-squared: 0.8992, Adjusted R-squared: 0.8975
#> F-statistic: 517.5 on 2 and 116 DF, p-value: < 2.2e-16Agora todas as variáveis tem indicação de significância estatística.
Confirmando o teste t com o teste F (ANOVA)
anova(mod5, mod4)#> Analysis of Variance Table
#>
#> Model 1: Vendas ~ TV + Radio
#> Model 2: Vendas ~ TV + Radio + Jornal
#> Res.Df RSS Df Sum of Sq F Pr(>F)
#> 1 116 299.47
#> 2 115 296.48 1 2.9906 1.16 0.2837Vamos comparar com o modelo só com TV
anova(mod1, mod5)#> Analysis of Variance Table
#>
#> Model 1: Vendas ~ TV
#> Model 2: Vendas ~ TV + Radio
#> Res.Df RSS Df Sum of Sq F Pr(>F)
#> 1 117 1173.73
#> 2 116 299.47 1 874.26 338.65 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Veja que agora a diferença é significativa. O melhor modelo é o com TV e Radio (mod5)
Calculando o erro padrão do resíduo com amostra de teste
Comparando com a melhor regressão simples
Comparando valor real vs ajustado
conj_treino$Previsoes <- predict(mod5, data=conj_treino)
ggplot(conj_treino, aes(x=Previsoes, y=Vendas)) +
geom_point() +
geom_abline(color = "darkblue") +
ggtitle("Vendas vs. Previsões do modelo linear")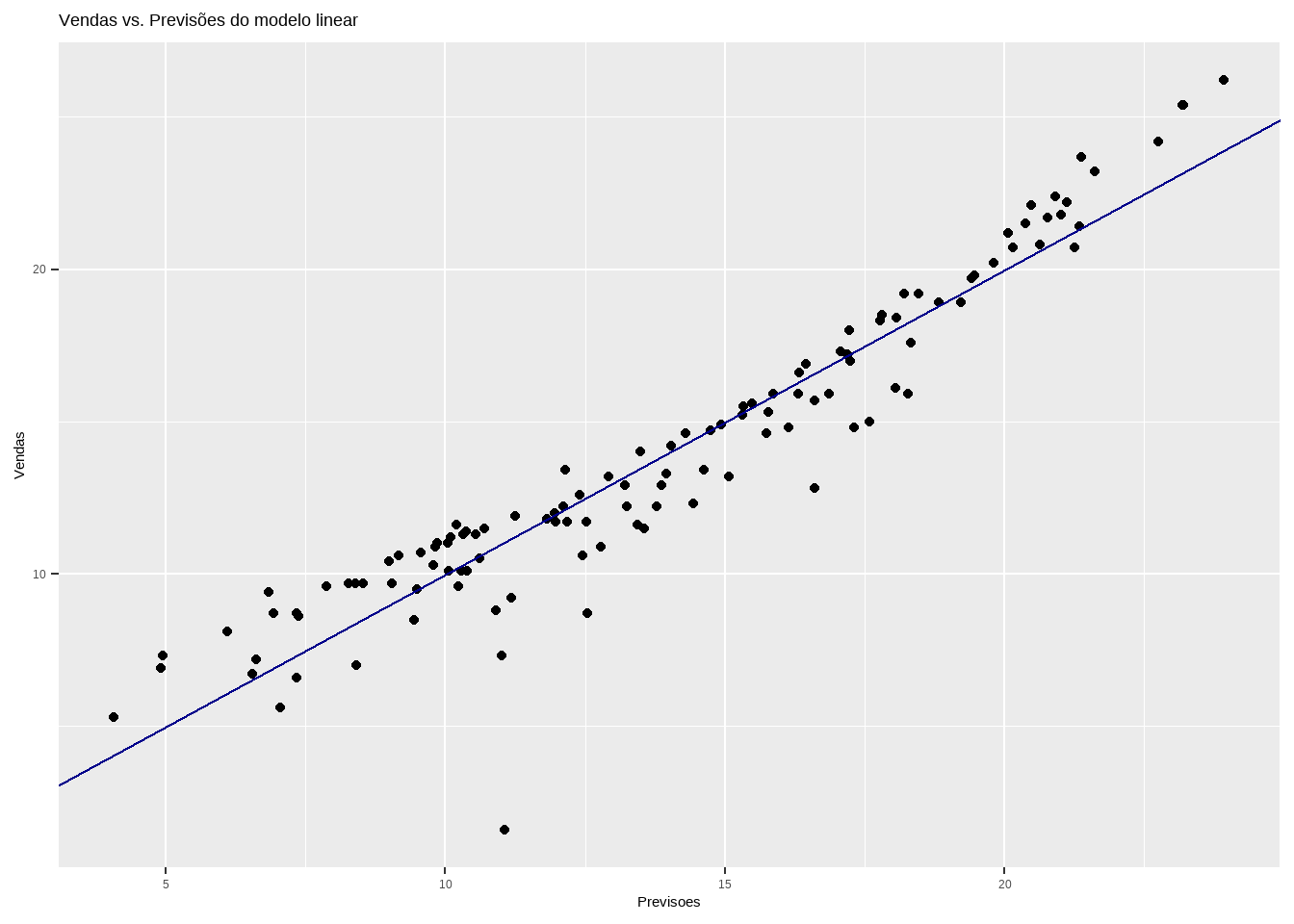
Análise Inicial dos Resíduos
Análise do Modelo - Parte 2
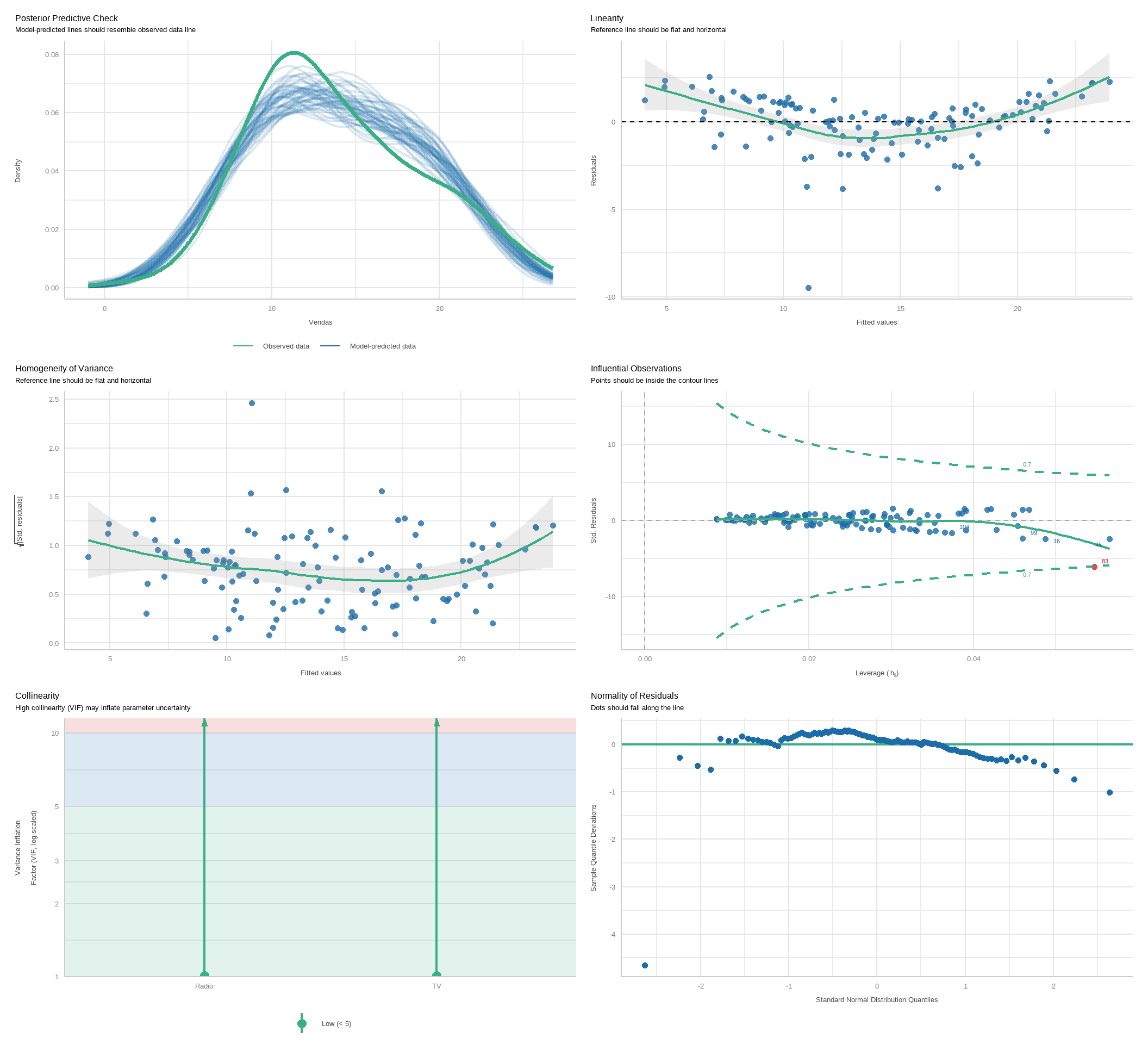
O pacote easystats tem uma função que faz uma análise mais detalhada do modelo. Os gráficos são mais fáceis de interpretar do que os obtidos com o plot do R base.
Análise do Modelo - Parte 3
O pacote car apresenta funções mais avançadas para análise de resíduos.
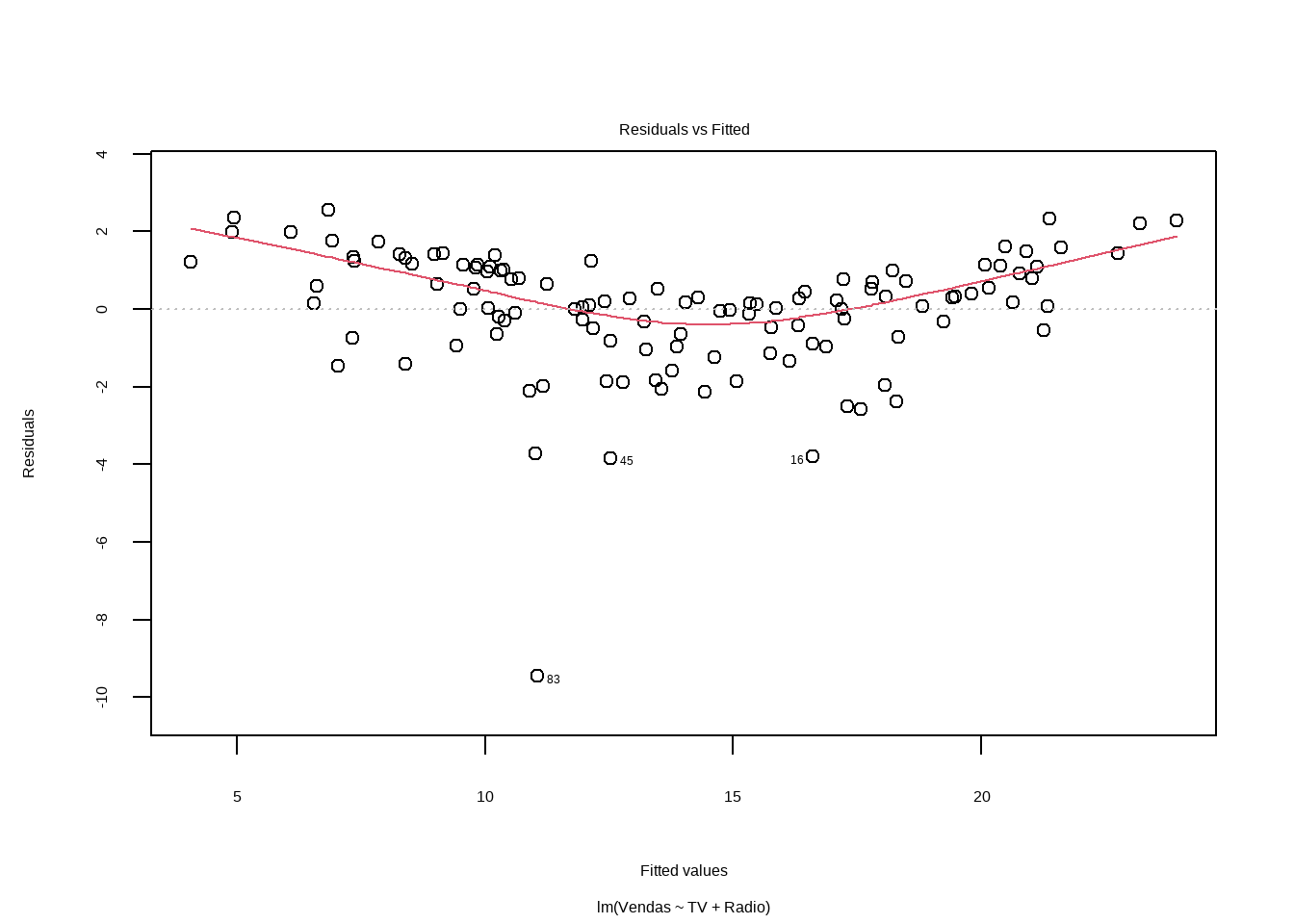
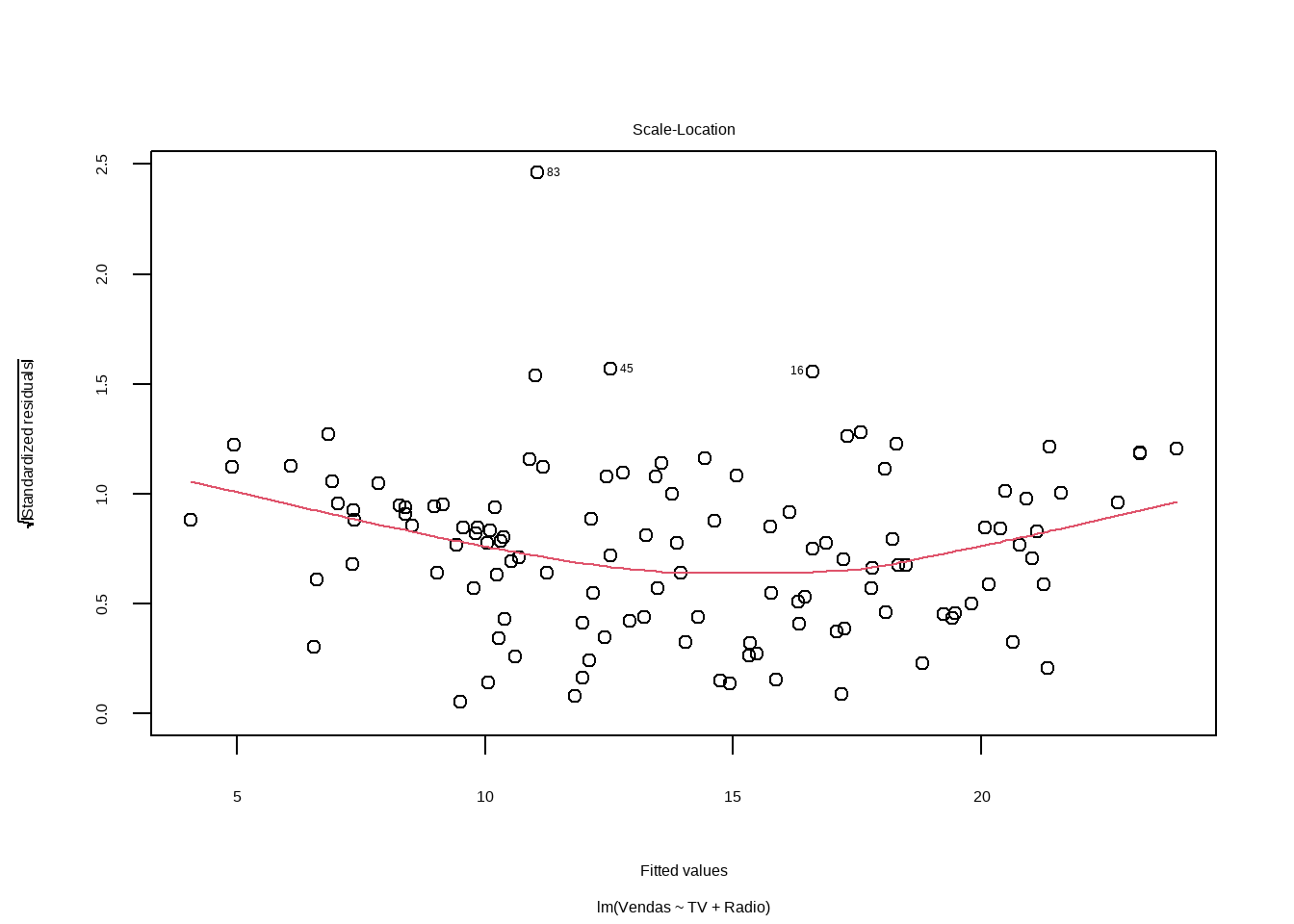
Para o gráfico de resíduos versus valores ajustados, podemos usar um teste chamado teste de Tukey de não aditividade (Tukey, 1949), ele é obtido adicionando os quadrados dos valores ajustados ao modelo e reajustando. O valor p para o teste de Tukey é obtido comparando a estatística de teste para a distribuição padrão-normal. O teste confirma a visível impressão de curvatura no gráfico residual, reforçando ainda mais a conclusão que o modelo não é adequado.
library(car)
residualPlots(mod5)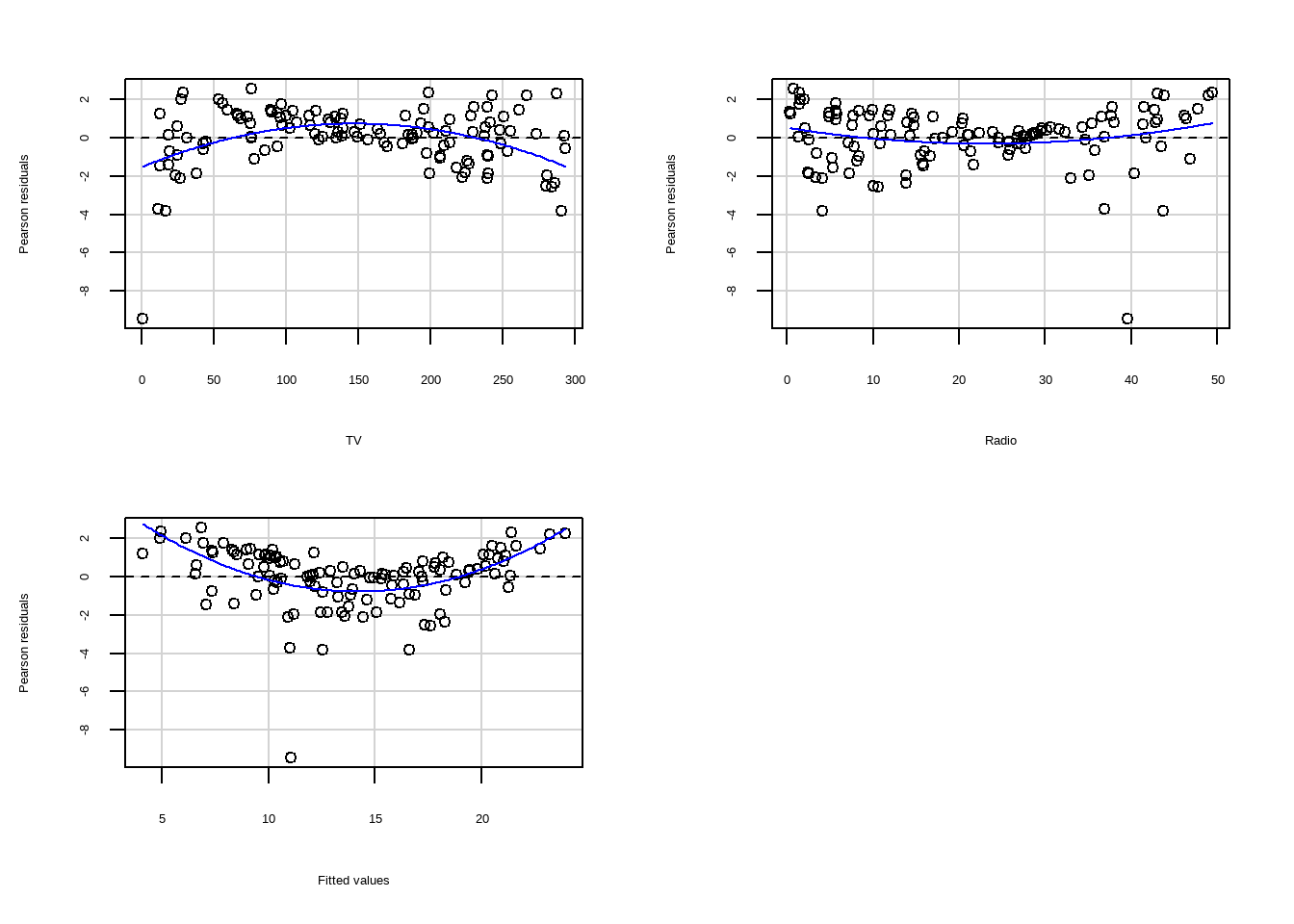
#> Test stat Pr(>|Test stat|)
#> TV -4.8383 4.102e-06 ***
#> Radio 1.9290 0.0562 .
#> Tukey test 6.4114 1.442e-10 ***
#> ---
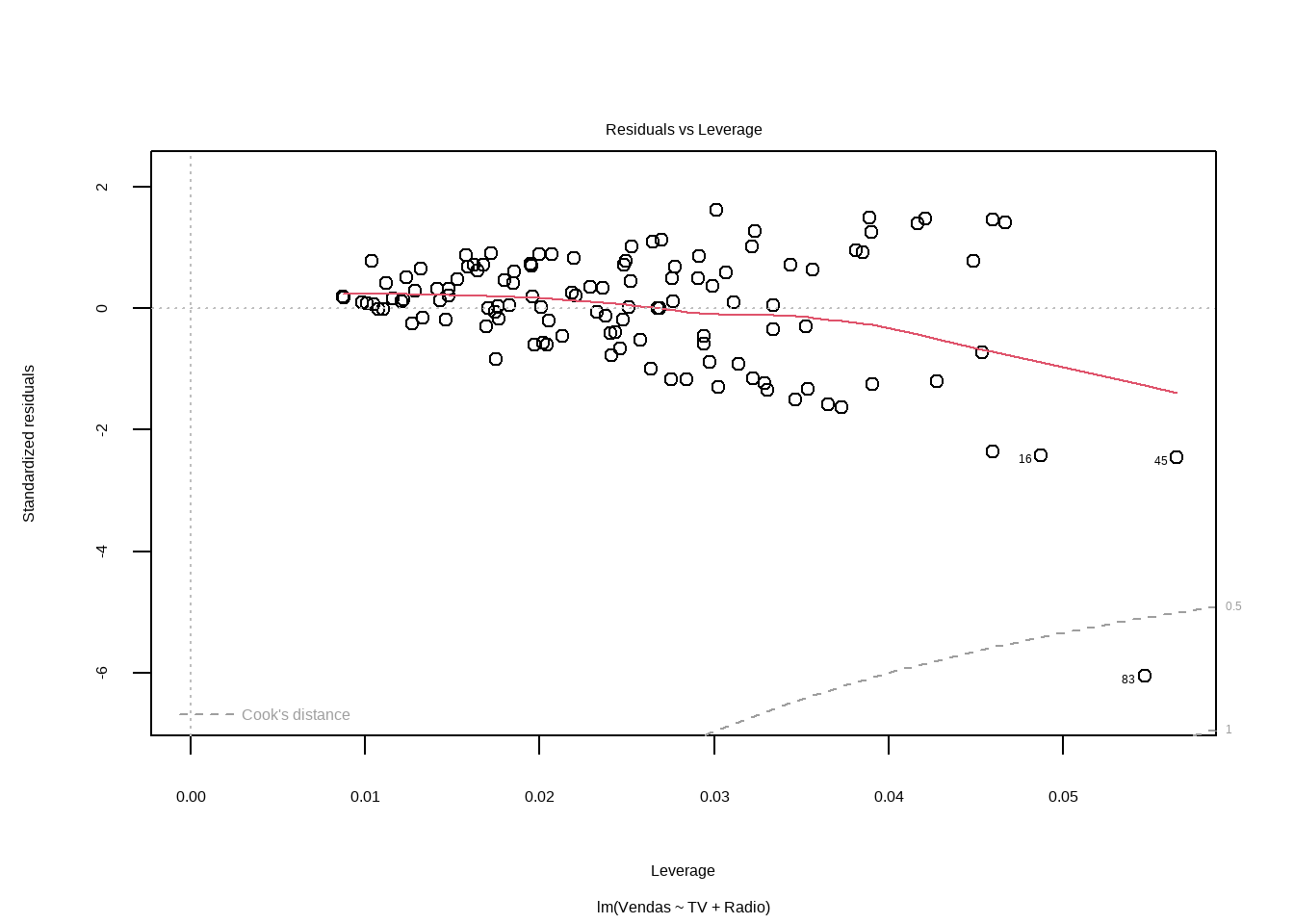
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1influencePlot(mod5)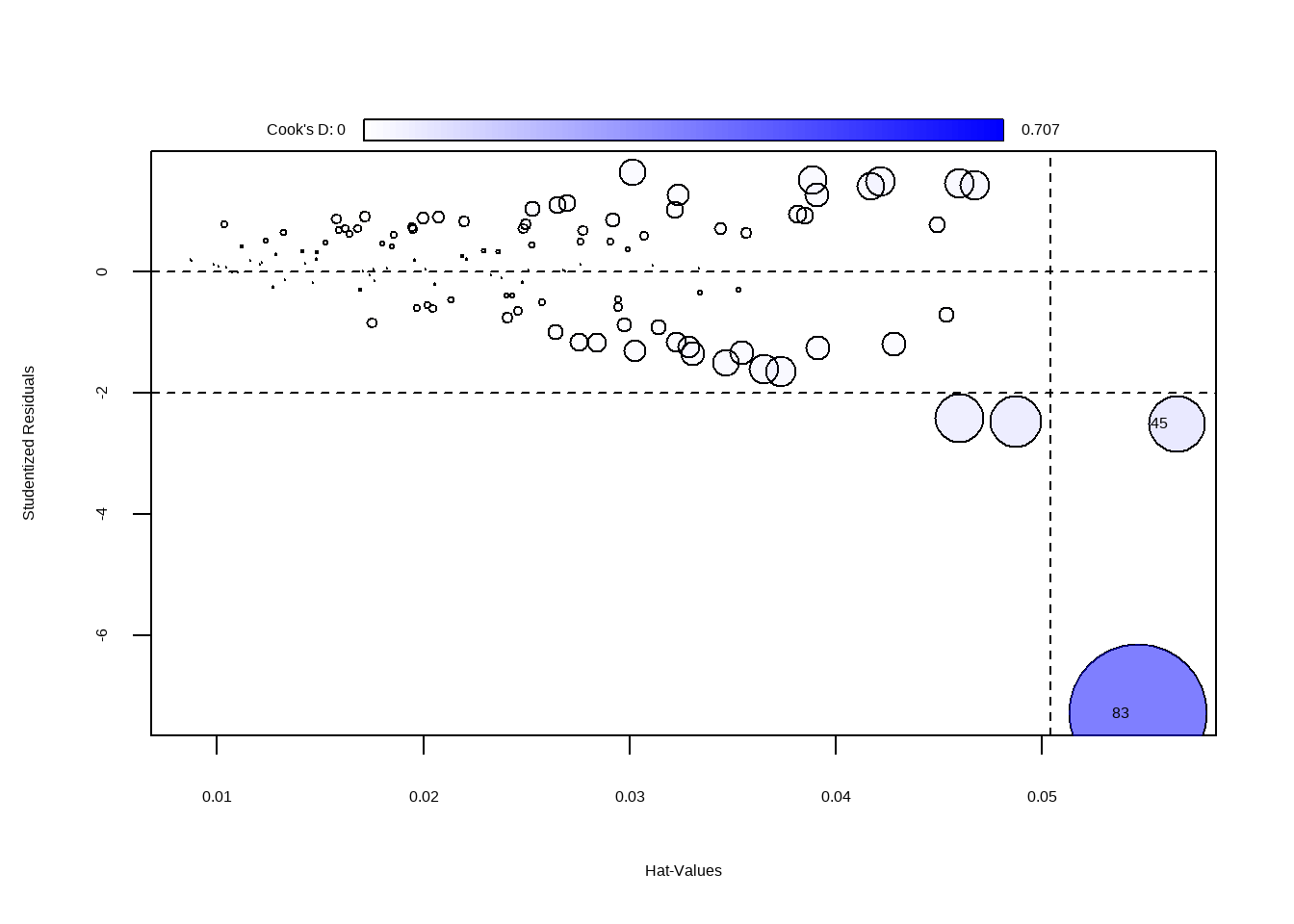
#> StudRes Hat CookD
#> 45 -2.512087 0.05650813 0.1204704
#> 83 -7.289206 0.05466694 0.7066190Tentando avaliar transformações
Aqui vamos avaliar a necessidade de transformar as variáveis para melhorar o modelo.
summary(p1 <- powerTransform(Vendas ~ TV + Radio, data=conj_treino))#> bcPower Transformation to Normality
#> Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
#> Y1 0.9937 1 0.8018 1.1856
#>
#> Likelihood ratio test that transformation parameter is equal to 0
#> (log transformation)
#> LRT df pval
#> LR test, lambda = (0) 111.042 1 < 2.22e-16
#>
#> Likelihood ratio test that no transformation is needed
#> LRT df pval
#> LR test, lambda = (1) 0.004149754 1 0.94864summary(p2 <- powerTransform(cbind(TV, Radio) ~1 , data=conj_treino))#> bcPower Transformations to Multinormality
#> Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
#> TV 0.7692 1.0 0.5311 1.0073
#> Radio 0.5349 0.5 0.3429 0.7269
#>
#> Likelihood ratio test that transformation parameters are equal to 0
#> (all log transformations)
#> LRT df pval
#> LR test, lambda = (0 0) 102.457 2 < 2.22e-16
#>
#> Likelihood ratio test that no transformations are needed
#> LRT df pval
#> LR test, lambda = (1 1) 22.189 2 1.5196e-05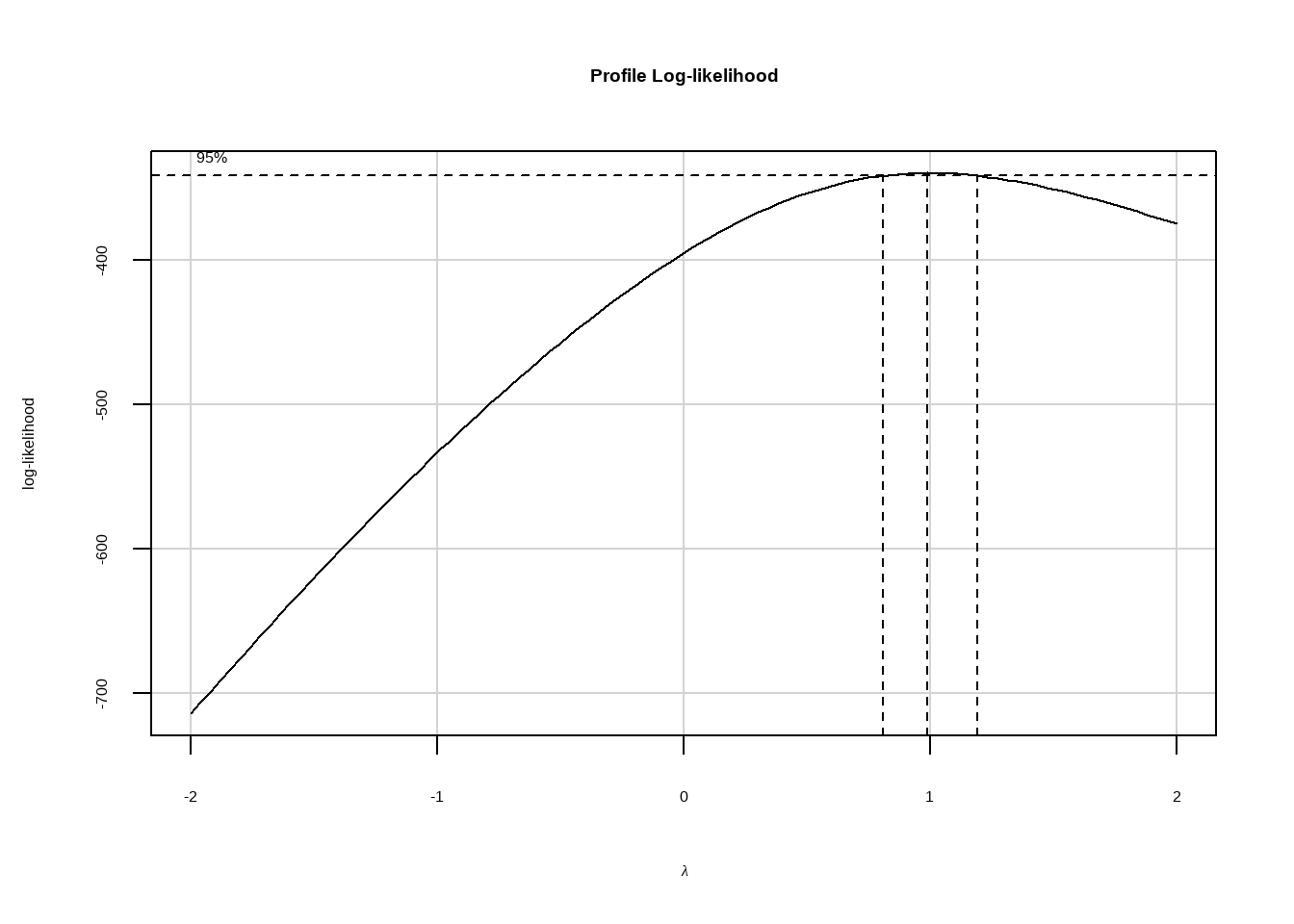
Análise do Modelo com car
# Fator de inflação da variância
vif(mod5)#> TV Radio
#> 1.014454 1.014454Teste dos resíduos
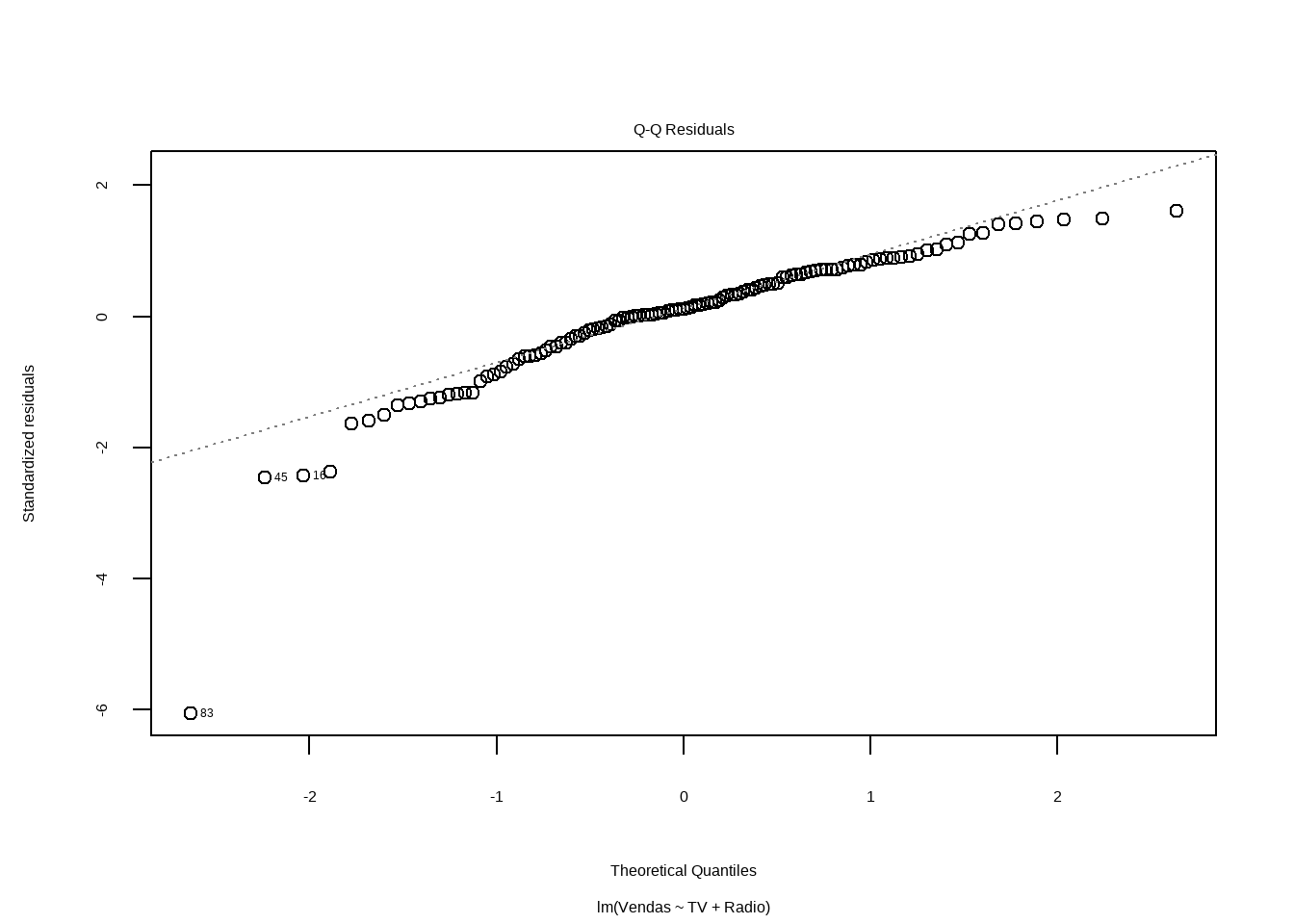
Teste de normalidade Teste de heterocedasticidade (Bresch-Pagan) Teste de autocorrelação (Durbin-Watson)
library(lmtest)#> Carregando pacotes exigidos: zoo#>
#> Anexando pacote: 'zoo'#> Os seguintes objetos são mascarados por 'package:base':
#>
#> as.Date, as.Date.numericmod5_sum <- summary(mod5)
# Teste de normalidade
shapiro.test(mod5_sum$residuals)#>
#> Shapiro-Wilk normality test
#>
#> data: mod5_sum$residuals
#> W = 0.8645, p-value = 4.88e-09# Teste de heterocedasticidade
bptest(mod5)#>
#> studentized Breusch-Pagan test
#>
#> data: mod5
#> BP = 4.9152, df = 2, p-value = 0.08564#Teste de autocorrelação
dwtest(mod5)#>
#> Durbin-Watson test
#>
#> data: mod5
#> DW = 2.1717, p-value = 0.8286
#> alternative hypothesis: true autocorrelation is greater than 0Dado que parece outlier e é um valor influente
A função OutlierTest () no pacote do car localiza o maior resíduo studentizado em valor absoluto e calcula o teste t com correção de Bonferroni. O testes de Outlier utiliza uma distribuição t para testar se o maior valor do residuo studentizado do modelo é estatisticamente diferente das outras observações. Um valor p significativo indica um outlier extremo que merece um exame mais aprofundado.
outlierTest(mod5)#> rstudent unadjusted p-value Bonferroni p
#> 83 -7.289206 4.2486e-11 5.0558e-09conj_treino[83,]#> # A tibble: 1 × 5
#> TV Radio Jornal Vendas Previsoes
#> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0.7 39.6 8.7 1.6 11.1