Classificação - Primeiros Passos

Author

Ricardo Accioly

Published

November 11, 2025

Primeiros Passos

Carregando Bibliotecas

library(tidyverse)
library(caret)
library(dslabs)
data(heights)

Traduzindo

head(heights)

#>      sex height
#> 1   Male     75
#> 2   Male     70
#> 3   Male     68
#> 4   Male     74
#> 5   Male     61
#> 6 Female     65

str(heights)

#> 'data.frame':    1050 obs. of  2 variables:
#>  $ sex   : Factor w/ 2 levels "Female","Male": 2 2 2 2 2 1 1 1 1 2 ...
#>  $ height: num  75 70 68 74 61 65 66 62 66 67 ...

alturas <- heights %>%
  # traduz dados para o português e transforma polegada para metro
  mutate(
          sex = case_when(
                           sex == "Male" ~ "Masculino",
                           sex == "Female" ~ "Feminino"
                          ), 
          altura = height * 2.54 / 100 ) %>%
  rename( sexo = sex) %>% 
  select(sexo , altura)
head(alturas)

#>        sexo altura
#> 1 Masculino 1.9050
#> 2 Masculino 1.7780
#> 3 Masculino 1.7272
#> 4 Masculino 1.8796
#> 5 Masculino 1.5494
#> 6  Feminino 1.6510

str(alturas)

#> 'data.frame':    1050 obs. of  2 variables:
#>  $ sexo  : chr  "Masculino" "Masculino" "Masculino" "Masculino" ...
#>  $ altura: num  1.9 1.78 1.73 1.88 1.55 ...

Alterando

alturas <- data.frame(sexo = factor(alturas$sexo), altura = alturas$altura)
str(alturas)

#> 'data.frame':    1050 obs. of  2 variables:
#>  $ sexo  : Factor w/ 2 levels "Feminino","Masculino": 2 2 2 2 2 1 1 1 1 2 ...
#>  $ altura: num  1.9 1.78 1.73 1.88 1.55 ...

head(alturas)

#>        sexo altura
#> 1 Masculino 1.9050
#> 2 Masculino 1.7780
#> 3 Masculino 1.7272
#> 4 Masculino 1.8796
#> 5 Masculino 1.5494
#> 6  Feminino 1.6510

Definindo x e y

y <- alturas$sexo
x <- alturas$altura

Treino e Teste

set.seed(1234)
indice_teste <- createDataPartition(y, times = 1, p = 0.2, list = FALSE)
conj_teste <- alturas[indice_teste, ]
conj_treino <- alturas[-indice_teste, ]
head(conj_teste)

#>         sexo altura
#> 4  Masculino 1.8796
#> 7   Feminino 1.6764
#> 9   Feminino 1.6764
#> 14 Masculino 1.7272
#> 16 Masculino 1.6764
#> 25 Masculino 1.8288

str(conj_teste)

#> 'data.frame':    211 obs. of  2 variables:
#>  $ sexo  : Factor w/ 2 levels "Feminino","Masculino": 2 1 1 2 2 2 2 2 2 2 ...
#>  $ altura: num  1.88 1.68 1.68 1.73 1.68 ...

summary(conj_teste)

#>         sexo         altura     
#>  Feminino : 48   Min.   :1.366  
#>  Masculino:163   1st Qu.:1.676  
#>                  Median :1.727  
#>                  Mean   :1.735  
#>                  3rd Qu.:1.803  
#>                  Max.   :2.032

head(conj_treino)

#>        sexo altura
#> 1 Masculino 1.9050
#> 2 Masculino 1.7780
#> 3 Masculino 1.7272
#> 5 Masculino 1.5494
#> 6  Feminino 1.6510
#> 8  Feminino 1.5748

str(conj_treino)

#> 'data.frame':    839 obs. of  2 variables:
#>  $ sexo  : Factor w/ 2 levels "Feminino","Masculino": 2 2 2 2 1 1 2 2 2 2 ...
#>  $ altura: num  1.9 1.78 1.73 1.55 1.65 ...

summary(conj_treino)

#>         sexo         altura     
#>  Feminino :190   Min.   :1.270  
#>  Masculino:649   1st Qu.:1.676  
#>                  Median :1.750  
#>                  Mean   :1.736  
#>                  3rd Qu.:1.803  
#>                  Max.   :2.100

Chutar a resposta!!!!!

Aqui vamos aletoriamente chutar a resposta.

y_chapeu <- sample(c("Masculino", "Feminino"), length(indice_teste), replace = TRUE) %>% 
  factor(levels = levels(conj_teste$sexo))

Calcula precisão

mean(y_chapeu == conj_teste$sexo)

#> [1] 0.549763

Melhorando

Agora vamos tentar melhorar o chute inicial usando as alturas das pessoas.

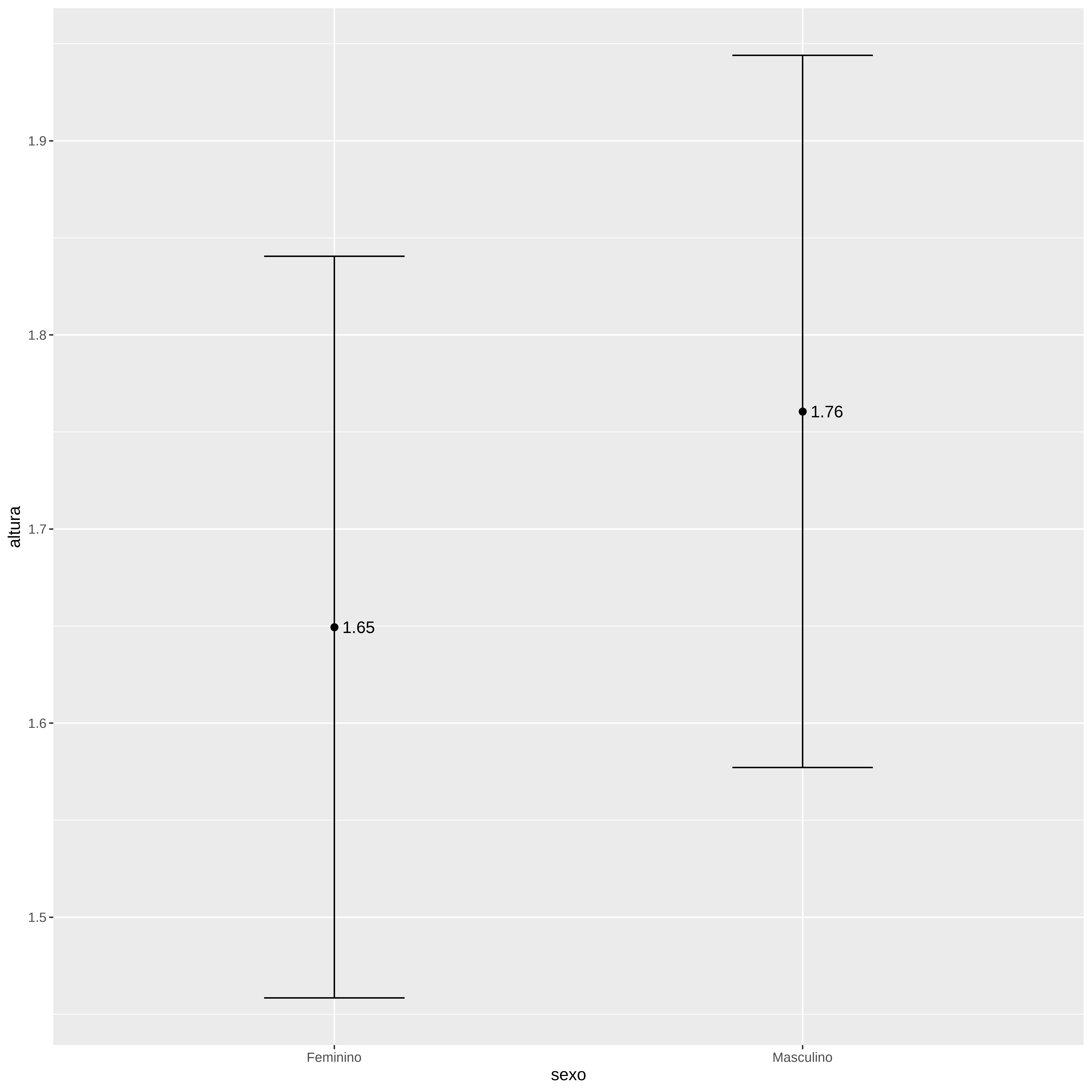
Primeiro vamos visualizar a distribuição das alturas entre homens e mulheres

library(ggplot2)
ggplot(alturas, aes(x = sexo, y = altura)) +
  stat_summary(
    geom = "errorbar",
    fun.max = function(y) mean(y) + 2*sd(y),
    fun.min = function(y) mean(y) - 2*sd(y),
    width = .3
  ) +
  stat_summary(
    geom = "point",
    fun = mean,
    size = 2
  ) +
  stat_summary(
    geom = "text",
    fun = mean,
    aes(label = after_stat(round(y, 2))),
    hjust = -0.3
  )

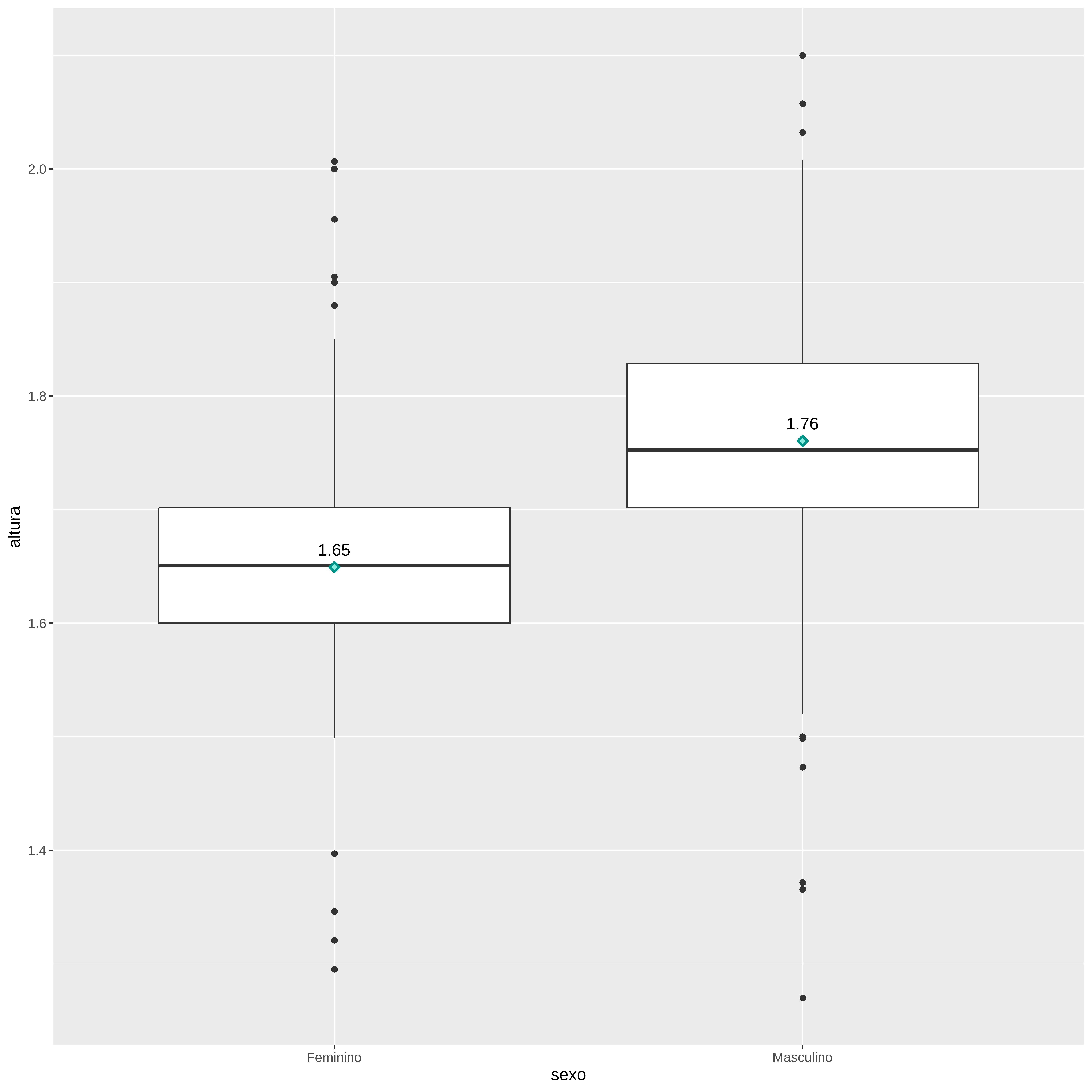
ggplot(alturas, aes(x = sexo, y = altura)) +
  geom_boxplot() +
  stat_summary(
    geom = "point",
    fun = mean,
    shape = 23,
    color = "#00978A",
    fill = "#88EBDD",
    stroke = 1.2
  ) +
  stat_summary(
    geom = "text",
    fun = mean,
    aes(label = after_stat(round(y, 2))),
    vjust = -1.0
  )

alturas %>% group_by(sexo) %>% summarize(mean(altura), sd(altura))

#> # A tibble: 2 × 3
#>   sexo      `mean(altura)` `sd(altura)`
#>   <fct>              <dbl>        <dbl>
#> 1 Feminino            1.65       0.0955
#> 2 Masculino           1.76       0.0917

media_Homem <- mean(alturas[alturas$sexo=="Masculino",]$altura)
desv_pad_Homem <- sd(alturas[alturas$sexo=="Masculino",]$altura)
media_Homem

#> [1] 1.760595

desv_pad_Homem

#> [1] 0.09172

media_Homem - 2*desv_pad_Homem

#> [1] 1.577155

y_chapeu <- ifelse(x > media_Homem - 2*desv_pad_Homem , "Masculino", "Feminino") %>% factor(levels = levels(conj_teste$sexo))
mean(y == y_chapeu)

#> [1] 0.7933333

Qual o melhor ponto de corte?

pontodecorte <- seq(1.54, 1.78, by = 0.01)
precisao <- map_dbl(pontodecorte, function(x){
  y_chapeu <- ifelse(conj_treino$altura > x, "Masculino", "Feminino") %>% 
    factor(levels = levels(conj_teste$sexo))
  mean(y_chapeu == conj_treino$sexo)
})
max(precisao)

#> [1] 0.8307509

melhor_ponto <- pontodecorte[which.max(precisao)]
melhor_ponto

#> [1] 1.65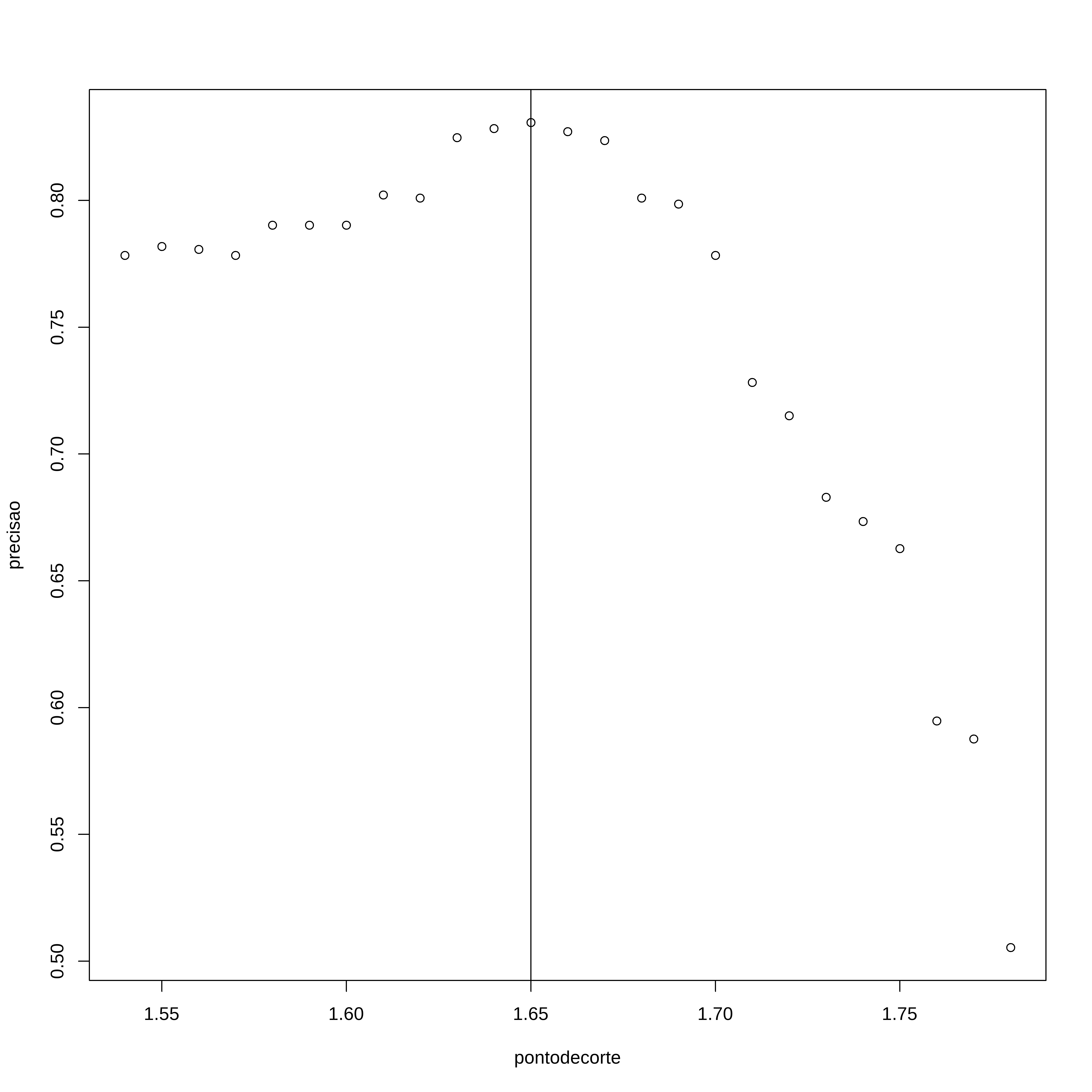

plot(pontodecorte, precisao) 
abline(v=melhor_ponto)

y_chapeu <- ifelse(conj_teste$altura > melhor_ponto, "Masculino", "Feminino") %>% 
  factor(levels = levels(conj_teste$sexo))
y_chapeu <- factor(y_chapeu)
mean(y_chapeu == conj_teste$sexo)

#> [1] 0.8530806

Melhorando o gráfico

library(ggplot2)
dados <- data.frame(pontodecorte, precisao)
ggplot(data=dados, aes(x=pontodecorte, y=precisao)) + geom_point() +
       geom_vline(xintercept = melhor_ponto, linetype="dashed", color="red")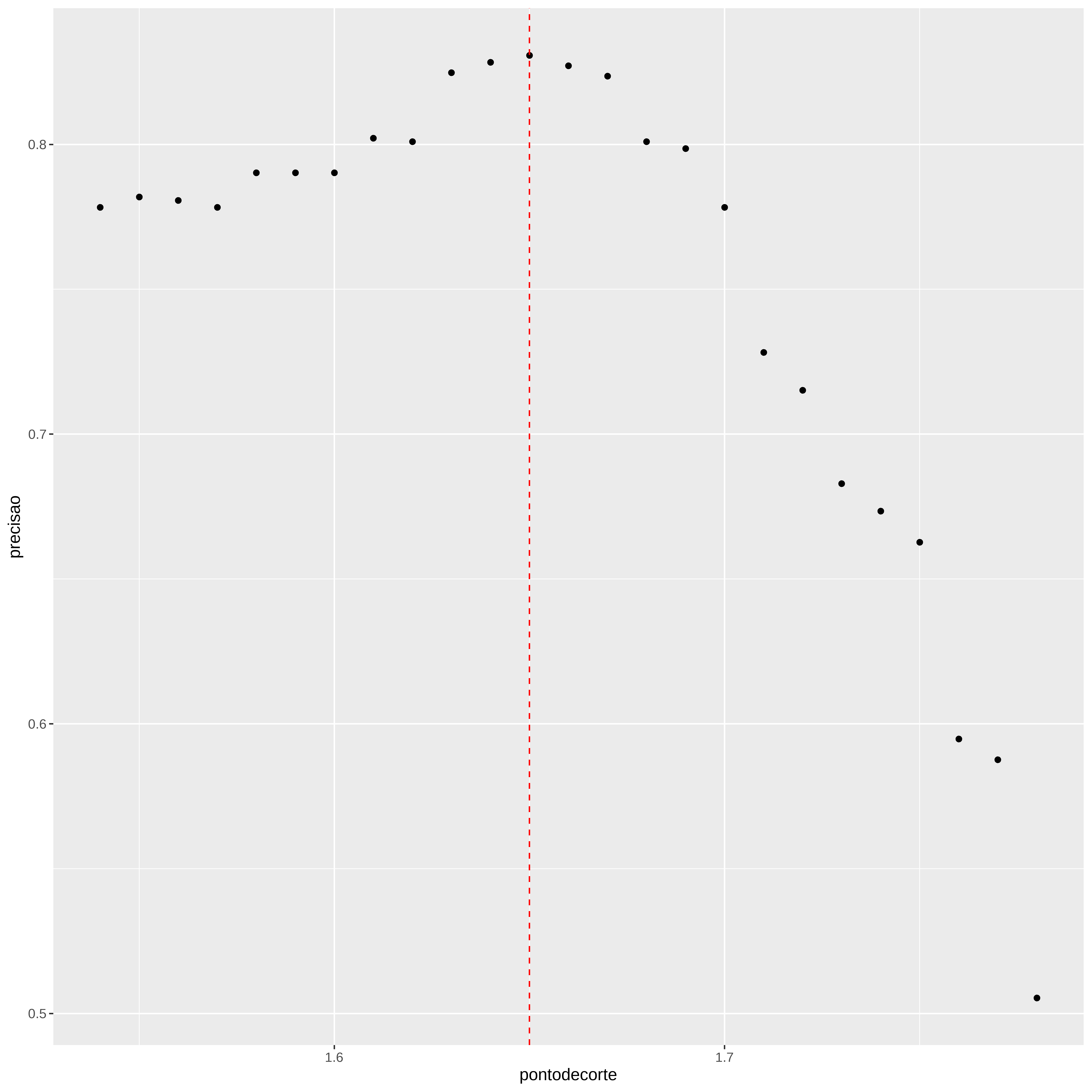

Matriz de Confusão

table(previsto = y_chapeu, real = conj_teste$sexo)

#>            real
#> previsto    Feminino Masculino
#>   Feminino        26         9
#>   Masculino       22       154

conj_teste %>% 
  mutate(y_chapeu = y_chapeu) %>%
  group_by(sexo) %>% 
  summarize(precisao = mean(y_chapeu == sexo))

#> # A tibble: 2 × 2
#>   sexo      precisao
#>   <fct>        <dbl>
#> 1 Feminino     0.542
#> 2 Masculino    0.945

confusionMatrix(data = y_chapeu, reference = conj_teste$sexo)

#> Confusion Matrix and Statistics
#> 
#>            Reference
#> Prediction  Feminino Masculino
#>   Feminino        26         9
#>   Masculino       22       154
#>                                          
#>                Accuracy : 0.8531         
#>                  95% CI : (0.798, 0.8979)
#>     No Information Rate : 0.7725         
#>     P-Value [Acc > NIR] : 0.002359       
#>                                          
#>                   Kappa : 0.5378         
#>                                          
#>  Mcnemar's Test P-Value : 0.031141       
#>                                          
#>             Sensitivity : 0.5417         
#>             Specificity : 0.9448         
#>          Pos Pred Value : 0.7429         
#>          Neg Pred Value : 0.8750         
#>              Prevalence : 0.2275         
#>          Detection Rate : 0.1232         
#>    Detection Prevalence : 0.1659         
#>       Balanced Accuracy : 0.7432         
#>                                          
#>        'Positive' Class : Feminino       
#>

Maximizando a estatística F1

pontodecorte <- seq(1.54, 1.78, by = 0.01)
F_1 <- map_dbl(pontodecorte, function(x){
  y_chapeu <- ifelse(conj_treino$altura > x, "Masculino", "Feminino") %>% 
    factor(levels = levels(conj_teste$sexo))
  F_meas(data = y_chapeu, reference = factor(conj_treino$sexo))
})
max(F_1)

#> [1] 0.616092

melhor_ponto <- pontodecorte[which.max(F_1)]
melhor_ponto

#> [1] 1.68

dados <- data.frame(pontodecorte, F_1)
ggplot(data=dados, aes(x=pontodecorte, y=F_1)) + geom_point() +
       geom_vline(xintercept = melhor_ponto, linetype="dashed", color="red")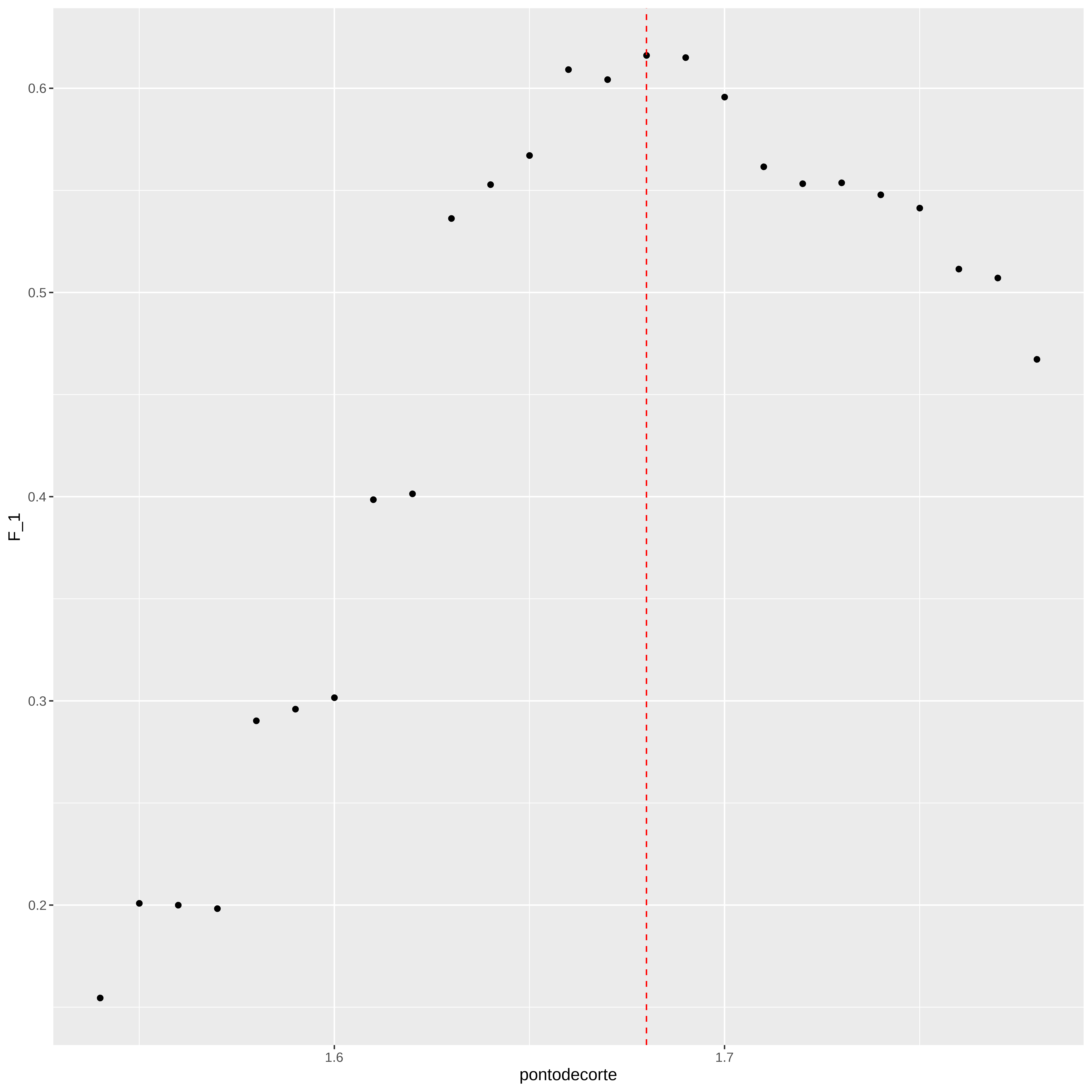

y_chapeu <- ifelse(conj_teste$altura > melhor_ponto, "Masculino", "Feminino") %>% 
  factor(levels = levels(conj_teste$sexo))
confusionMatrix(data = y_chapeu, reference = conj_teste$sexo)

#> Confusion Matrix and Statistics
#> 
#>            Reference
#> Prediction  Feminino Masculino
#>   Feminino        32        26
#>   Masculino       16       137
#>                                           
#>                Accuracy : 0.8009          
#>                  95% CI : (0.7406, 0.8526)
#>     No Information Rate : 0.7725          
#>     P-Value [Acc > NIR] : 0.1839          
#>                                           
#>                   Kappa : 0.4724          
#>                                           
#>  Mcnemar's Test P-Value : 0.1649          
#>                                           
#>             Sensitivity : 0.6667          
#>             Specificity : 0.8405          
#>          Pos Pred Value : 0.5517          
#>          Neg Pred Value : 0.8954          
#>              Prevalence : 0.2275          
#>          Detection Rate : 0.1517          
#>    Detection Prevalence : 0.2749          
#>       Balanced Accuracy : 0.7536          
#>                                           
#>        'Positive' Class : Feminino        
#>

Voltando a chutar

p <- 0.9
y_chapeu <- sample(c("Masculino", "Feminino"), length(indice_teste), 
                   replace = TRUE, prob=c(p, 1-p)) %>% factor(levels = levels(conj_teste$sexo))
mean(y_chapeu == conj_teste$sexo)

#> [1] 0.6919431

Curva ROC

     ggplot() +
     geom_abline(intercept = 0, slope = 1.) + 
     labs(x = "Taxa Positiva Falsa (1 - Especificidade)", 
          y = "Taxa Positiva Verdadeira (Sensibilidade)", 
          title = "Curva ROC") +
     scale_x_continuous(limits = c(0, 1.0)) + 
     scale_y_continuous(limits = c(0, 1.0))

Testando probabilidades

probs <- seq(0, 1, length.out = 10)
chutando <- map_df(probs, function(p){
     y_chapeu <- 
          sample(c("Masculino", "Feminino"), length(indice_teste), replace = TRUE,                            prob=c(p, 1-p)) %>%  factor(levels = levels(conj_teste$sexo))
      list(metodo = "Chutando",
           TPF = 1 - specificity(y_chapeu, conj_teste$sexo),
           TPV = sensitivity(y_chapeu, conj_teste$sexo)) 
})
     chutando %>%
     ggplot(aes(TPF, TPV)) +
     geom_line() +
     geom_point() +
     geom_abline(intercept = 0, slope = 1.) + 
     labs(x = "Taxa Positiva Falsa (1 - Especificidade)", 
          y = "Taxa Positiva Verdadeira (Sensibilidade)", 
          title = "Curva ROC Método Chutando") +
     scale_x_continuous(limits = c(0, 1.0)) + 
     scale_y_continuous(limits = c(0, 1.0))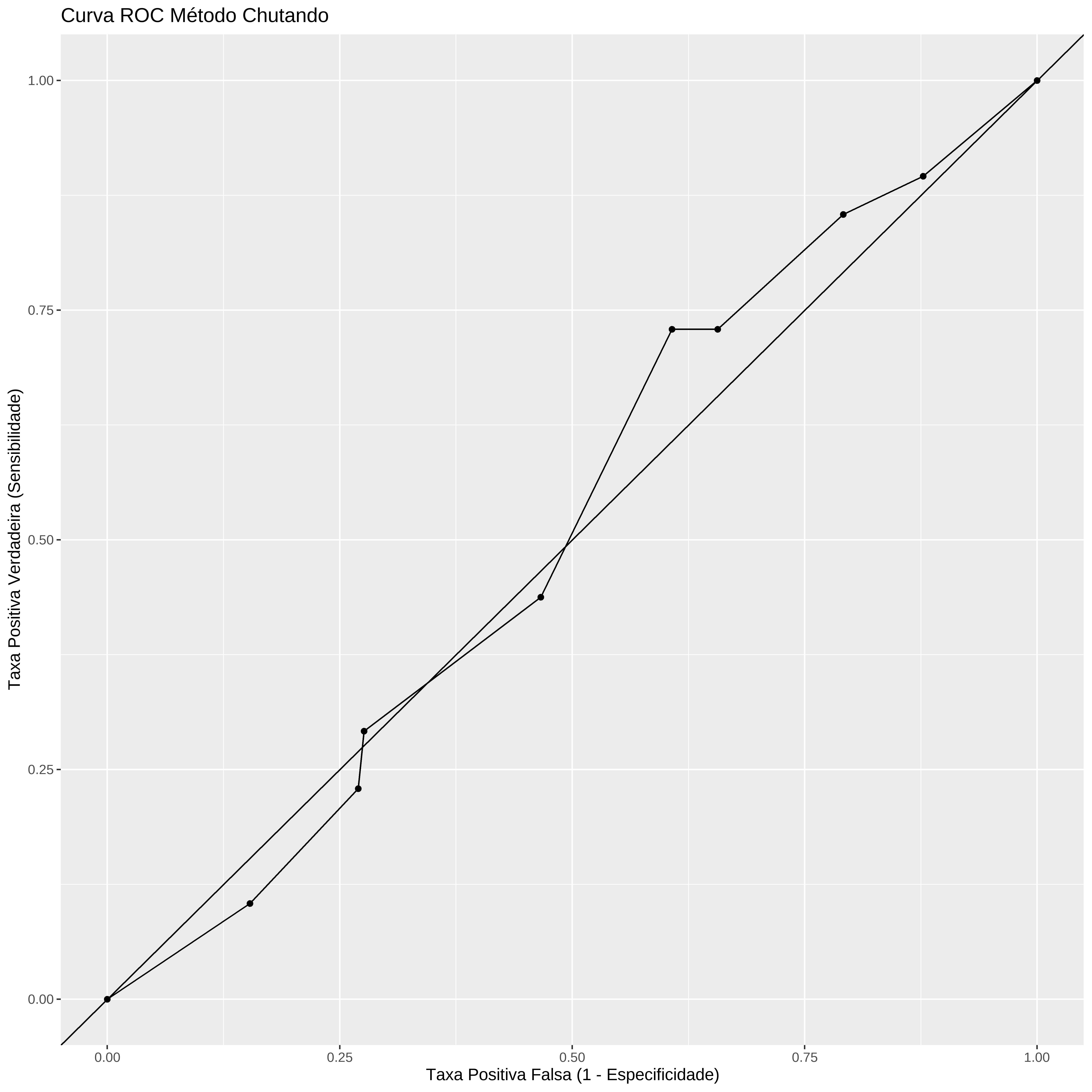

Comparando os dois métodos

pontodecorte <- seq(1.27 , 1.92, by = 0.01)
altura_ptdecorte <- map_df(pontodecorte, function(x){
     y_chapeu <- ifelse(conj_teste$altura > x, "Masculino", "Feminino") %>% 
                 factor(levels = levels(conj_teste$sexo))
     list(metodo = "Corte por Altura",
        TPF = 1 - specificity(y_chapeu, conj_teste$sexo),
        TPV = sensitivity(y_chapeu, conj_teste$sexo)) 
})
bind_rows(chutando, altura_ptdecorte) %>%
     ggplot(aes(TPF, TPV, color = metodo)) +
     geom_line() +
     geom_point() +
     geom_abline(intercept = 0, slope = 1.) + 
     labs(x = "Taxa Positiva Falsa (1 - Especificidade)", 
          y = "Taxa Positiva Verdadeira (Sensibilidade)", 
          title = "Curva ROC") +
     scale_x_continuous(limits = c(0, 1.0)) + 
     scale_y_continuous(limits = c(0, 1.0))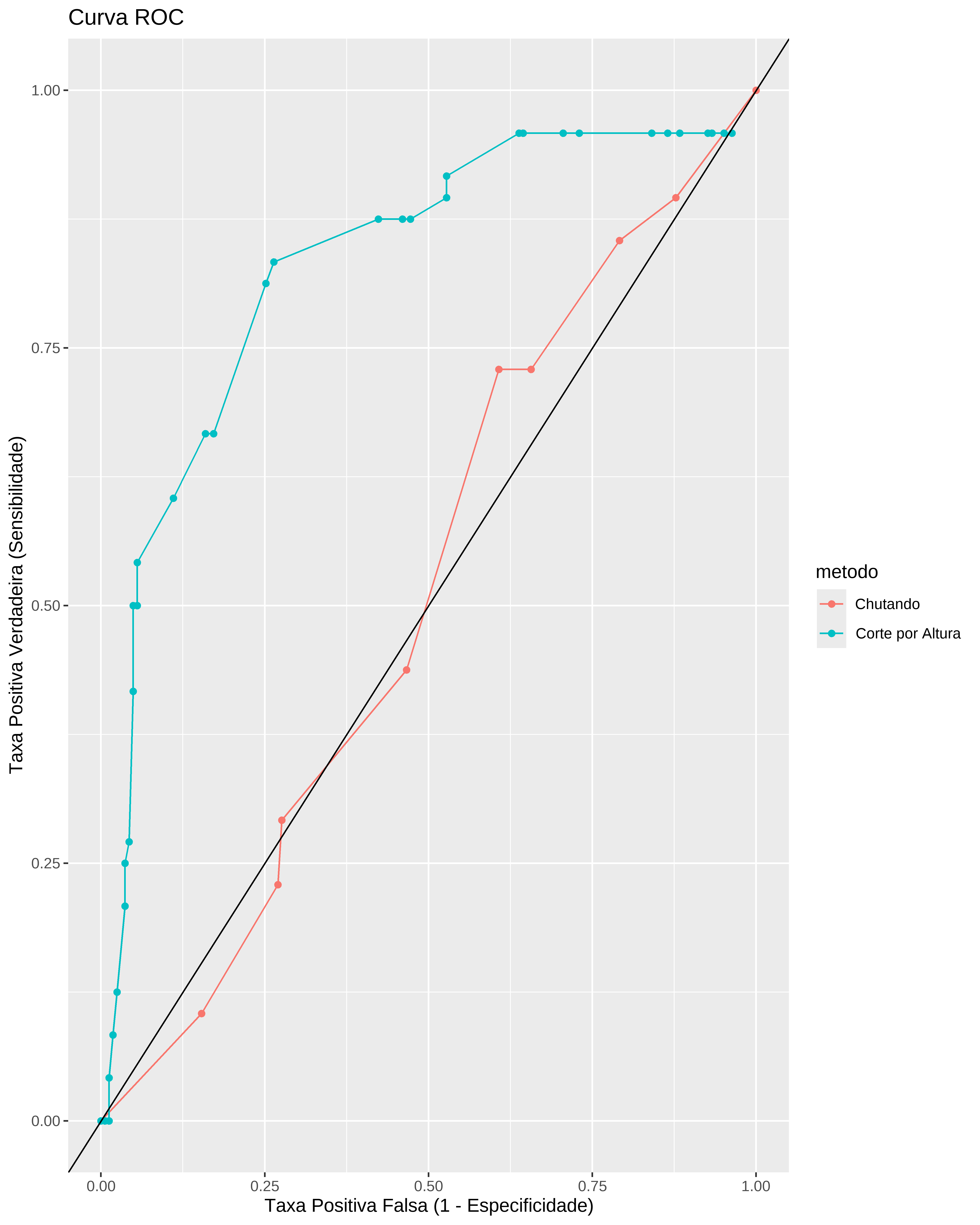

Pontos da curva ROC

map_df(pontodecorte, function(x){
     y_chapeu <- ifelse(conj_teste$altura > x, "Masculino", "Feminino") %>% 
                  factor(levels = c("Masculino", "Feminino"))
     list(metodo = "Corte por Altura",
          corte = round(x, 2), 
          TPF = 1 - specificity(y_chapeu, conj_teste$sexo),
          TPV = sensitivity(y_chapeu, conj_teste$sexo)) 
}) %>%
     ggplot(aes(TPF, TPV, label = corte)) +
     geom_line() +
     geom_point() +
     geom_text(nudge_y = - 0.05, size = 3, check_overlap = TRUE) +
     scale_x_continuous(limits = c(0, 1.0)) + 
     scale_y_continuous(limits = c(0, 1.0))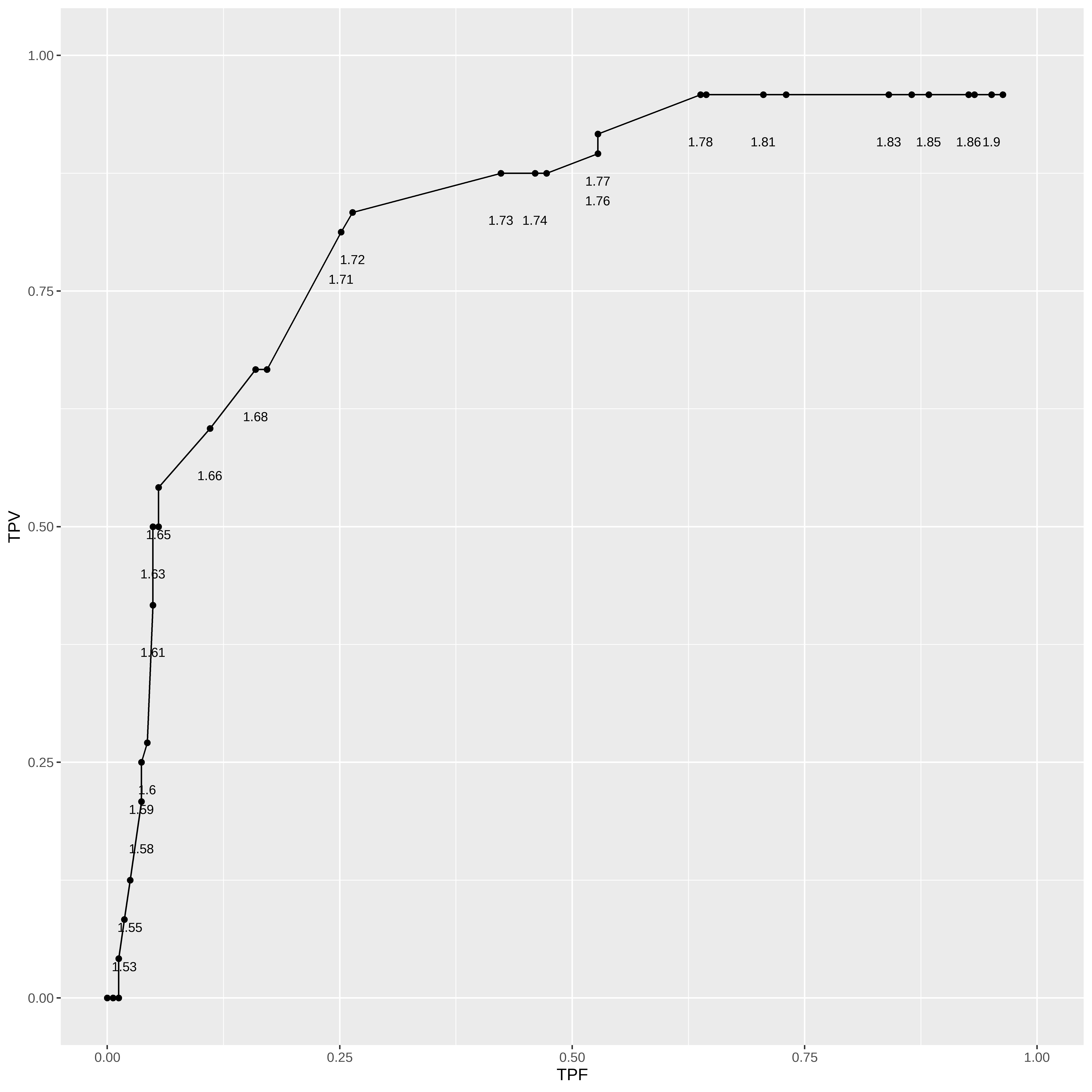

Bayes Ingênuo (Naive Bayes)

params <- conj_treino %>% 
     group_by(sexo) %>% 
     summarize(media = mean(altura), desvpad = sd(altura))
params

#> # A tibble: 2 × 3
#>   sexo      media desvpad
#>   <fct>     <dbl>   <dbl>
#> 1 Feminino   1.65  0.0947
#> 2 Masculino  1.76  0.0925

pi <- conj_treino %>% summarize(pi=mean(sexo=="Feminino")) %>% pull(pi)
pi

#> [1] 0.2264601

x <- conj_teste$altura

f1 <- dnorm(x, params$media[1], params$desvpad[1])
f0 <- dnorm(x, params$media[2], params$desvpad[2])

p_chapeu_bayes <- f1*pi / (f1*pi + f0*(1 - pi))
y_chapeu_bayes <- ifelse(p_chapeu_bayes > 0.5, "Feminino", "Masculino")

confusionMatrix(factor(y_chapeu_bayes), conj_teste$sexo,  positive="Feminino")

#> Confusion Matrix and Statistics
#> 
#>            Reference
#> Prediction  Feminino Masculino
#>   Feminino        20         7
#>   Masculino       28       156
#>                                           
#>                Accuracy : 0.8341          
#>                  95% CI : (0.7769, 0.8817)
#>     No Information Rate : 0.7725          
#>     P-Value [Acc > NIR] : 0.0174801       
#>                                           
#>                   Kappa : 0.4419          
#>                                           
#>  Mcnemar's Test P-Value : 0.0007232       
#>                                           
#>             Sensitivity : 0.41667         
#>             Specificity : 0.95706         
#>          Pos Pred Value : 0.74074         
#>          Neg Pred Value : 0.84783         
#>              Prevalence : 0.22749         
#>          Detection Rate : 0.09479         
#>    Detection Prevalence : 0.12796         
#>       Balanced Accuracy : 0.68686         
#>                                           
#>        'Positive' Class : Feminino        
#>