Regressão Linear

Author

Ricardo Accioly

Published

April 28, 2025

Carregando bibliotecas

#> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr     1.1.4     ✔ readr     2.1.5
#> ✔ forcats   1.0.0     ✔ stringr   1.5.1
#> ✔ ggplot2   3.5.2     ✔ tibble    3.2.1
#> ✔ lubridate 1.9.4     ✔ tidyr     1.3.1
#> ✔ purrr     1.0.4     
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag()    masks stats::lag()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Dados de propaganda

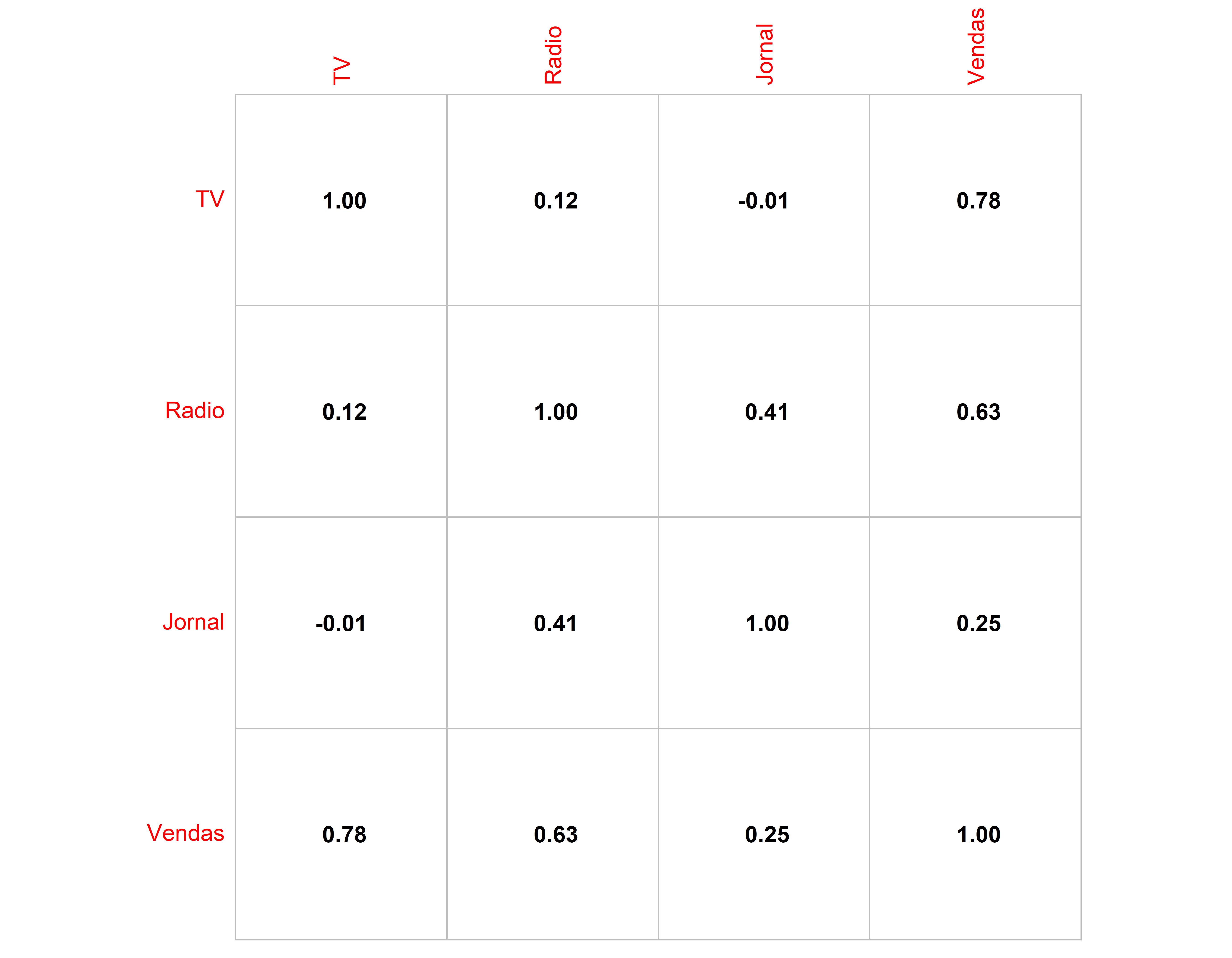
O conjunto de dados contém estatísticas sobre as vendas de um produto em 200 diferentes mercados, juntamente com orçamentos publicitários em cada um desses mercados, para diferentes canais de mídia: TV, rádio e jornal. As vendas estão em milhares de unidades e o orçamento está em milhares de dólares.

library(readxl)
propaganda <- read_excel("Propaganda.xlsx")
summary(propaganda)
#>        TV             Radio          Newspaper          Sales      
#>  Min.   :  0.70   Min.   : 0.000   Min.   :  0.30   Min.   : 1.60  
#>  1st Qu.: 74.38   1st Qu.: 9.975   1st Qu.: 12.75   1st Qu.:10.38  
#>  Median :149.75   Median :22.900   Median : 25.75   Median :12.90  
#>  Mean   :147.04   Mean   :23.264   Mean   : 30.55   Mean   :14.02  
#>  3rd Qu.:218.82   3rd Qu.:36.525   3rd Qu.: 45.10   3rd Qu.:17.40  
#>  Max.   :296.40   Max.   :49.600   Max.   :114.00   Max.   :27.00

Renomeando

propaganda <- propaganda %>% rename(Jornal = Newspaper, Vendas = Sales)

Sumario

#> 
#> Anexando pacote: 'summarytools'
#> O seguinte objeto é mascarado por 'package:tibble':
#> 
#>     view
dfSummary(propaganda) |> stview(method = "render")

Data Frame Summary

propaganda

Dimensions: 200 x 4
Duplicates: 0
No Variable Stats / Values Freqs (% of Valid) Graph Valid Missing
1 TV [numeric]
Mean (sd) : 147 (85.9)
min ≤ med ≤ max:
0.7 ≤ 149.8 ≤ 296.4
IQR (CV) : 144.4 (0.6)
190 distinct values 200 (100.0%) 0 (0.0%)
2 Radio [numeric]
Mean (sd) : 23.3 (14.8)
min ≤ med ≤ max:
0 ≤ 22.9 ≤ 49.6
IQR (CV) : 26.5 (0.6)
167 distinct values 200 (100.0%) 0 (0.0%)
3 Jornal [numeric]
Mean (sd) : 30.6 (21.8)
min ≤ med ≤ max:
0.3 ≤ 25.8 ≤ 114
IQR (CV) : 32.4 (0.7)
172 distinct values 200 (100.0%) 0 (0.0%)
4 Vendas [numeric]
Mean (sd) : 14 (5.2)
min ≤ med ≤ max:
1.6 ≤ 12.9 ≤ 27
IQR (CV) : 7 (0.4)
121 distinct values 200 (100.0%) 0 (0.0%)

Generated by summarytools 1.1.3 (R version 4.5.0)
2025-04-28

Linhas inicias

library(gt)
gt(head(propaganda, 10)) %>% 
  tab_header(title = "Propaganda")
Propaganda
TV Radio Jornal Vendas
230.1 37.8 69.2 22.1
44.5 39.3 45.1 10.4
17.2 45.9 69.3 9.3
151.5 41.3 58.5 18.5
180.8 10.8 58.4 12.9
8.7 48.9 75.0 7.2
57.5 32.8 23.5 11.8
120.2 19.6 11.6 13.2
8.6 2.1 1.0 4.8
199.8 2.6 21.2 10.6

Criando amostra de treino e teste

library(caret)
set.seed(21)
y <- propaganda$Vendas
indice_teste <- createDataPartition(y, times = 1, p = 0.40, list = FALSE)

conj_treino <- propaganda[-indice_teste, ]
conj_teste <- propaganda[indice_teste, ]

str(conj_treino)
#> tibble [119 × 4] (S3: tbl_df/tbl/data.frame)
#>  $ TV    : num [1:119] 230.1 151.5 180.8 199.8 66.1 ...
#>  $ Radio : num [1:119] 37.8 41.3 10.8 2.6 5.8 35.1 7.6 47.7 20.5 23.9 ...
#>  $ Jornal: num [1:119] 69.2 58.5 58.4 21.2 24.2 65.9 7.2 52.9 18.3 19.1 ...
#>  $ Vendas: num [1:119] 22.1 18.5 12.9 10.6 8.6 9.2 9.7 22.4 11.3 14.6 ...
str(conj_teste)
#> tibble [81 × 4] (S3: tbl_df/tbl/data.frame)
#>  $ TV    : num [1:81] 44.5 17.2 8.7 57.5 120.2 ...
#>  $ Radio : num [1:81] 39.3 45.9 48.9 32.8 19.6 2.1 24 32.9 36.6 39.6 ...
#>  $ Jornal: num [1:81] 45.1 69.3 75 23.5 11.6 1 4 46 114 55.8 ...
#>  $ Vendas: num [1:81] 10.4 9.3 7.2 11.8 13.2 4.8 17.4 19 12.5 24.4 ...
gt::gt(head(conj_treino, 10))   %>% 
  tab_header(title = "Propaganda")
Propaganda
TV Radio Jornal Vendas
230.1 37.8 69.2 22.1
151.5 41.3 58.5 18.5
180.8 10.8 58.4 12.9
199.8 2.6 21.2 10.6
66.1 5.8 24.2 8.6
23.8 35.1 65.9 9.2
97.5 7.6 7.2 9.7
195.4 47.7 52.9 22.4
69.2 20.5 18.3 11.3
147.3 23.9 19.1 14.6

Primeira visualização dos dados

Aqui estou usando uma função do pacote caret que de uma maneira simples apresenta a relação entre a variável resposta e suas possíveis variáveis explicativas

featurePlot(x = conj_treino[ , c("TV", "Radio", "Jornal")], y = conj_treino$Vendas)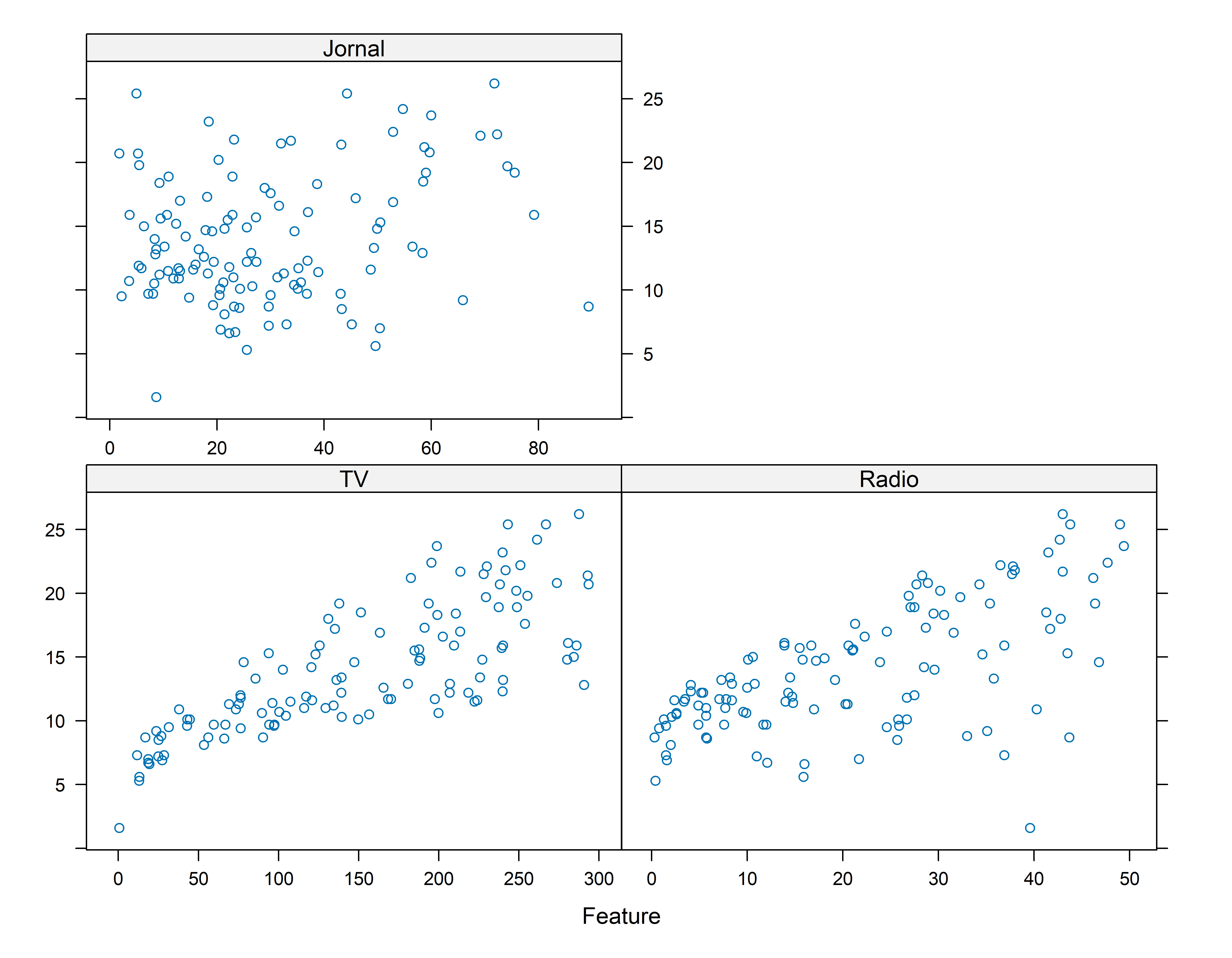

Usando o ggplot

gt(head(conj_treino, 10))
TV Radio Jornal Vendas
230.1 37.8 69.2 22.1
151.5 41.3 58.5 18.5
180.8 10.8 58.4 12.9
199.8 2.6 21.2 10.6
66.1 5.8 24.2 8.6
23.8 35.1 65.9 9.2
97.5 7.6 7.2 9.7
195.4 47.7 52.9 22.4
69.2 20.5 18.3 11.3
147.3 23.9 19.1 14.6 
c_treino_pivot <- conj_treino %>% pivot_longer(!Vendas, names_to="Tipo", values_to="Orçamento" ) 
gt(head(c_treino_pivot, 10))
Vendas Tipo Orçamento
22.1 TV 230.1
22.1 Radio 37.8
22.1 Jornal 69.2
18.5 TV 151.5
18.5 Radio 41.3
18.5 Jornal 58.5
12.9 TV 180.8
12.9 Radio 10.8
12.9 Jornal 58.4
10.6 TV 199.8 
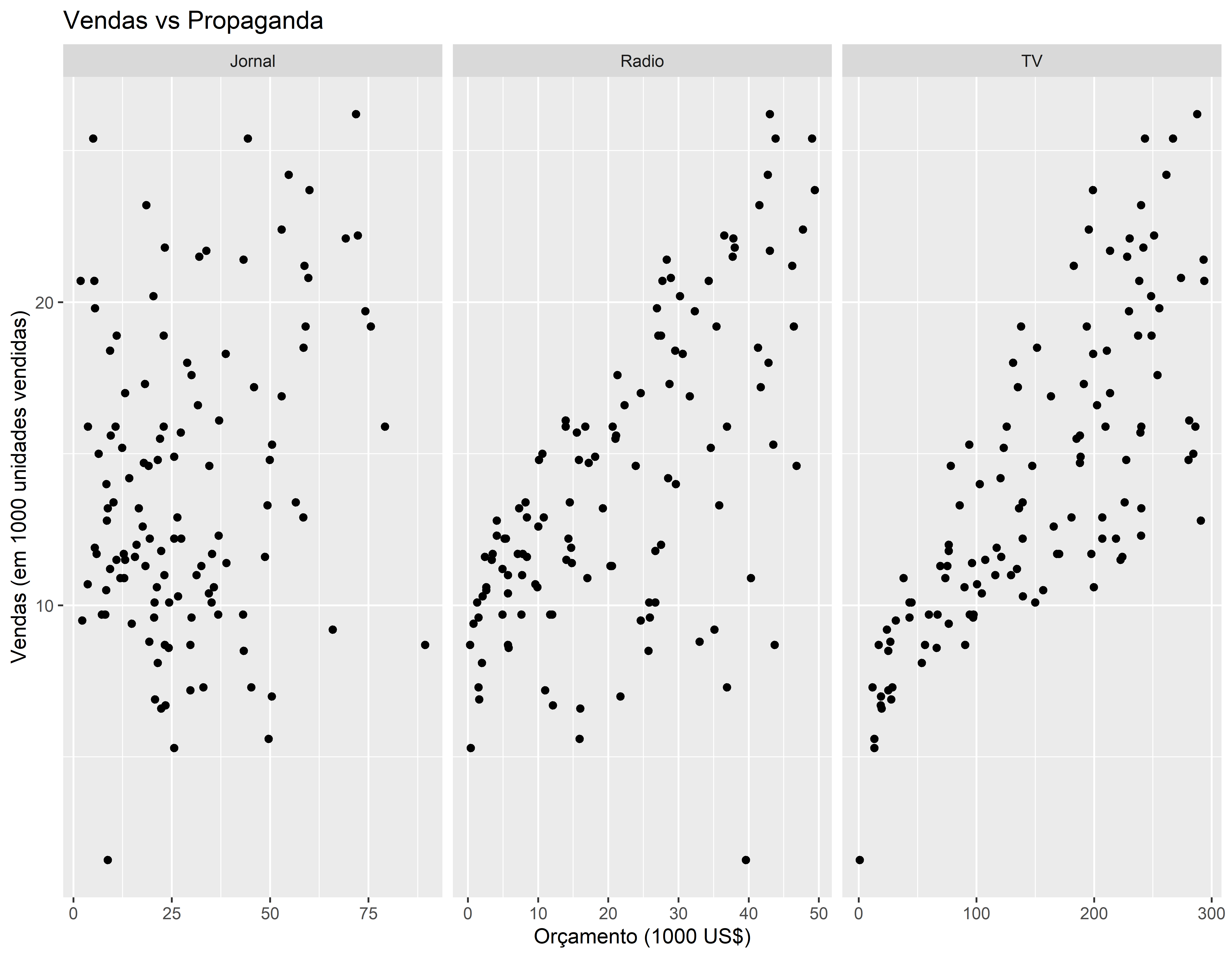
conj_treino %>% pivot_longer(!Vendas, names_to="Tipo", values_to="Orçamento" ) %>%
            ggplot() + 
            geom_point(aes(x=Orçamento, y=Vendas)) +
            facet_wrap( ~ Tipo, scales = "free_x") +
            labs(x = "Orçamento (1000 US$)", 
                 y = "Vendas (em 1000 unidades vendidas)", 
                 title = "Vendas vs Propaganda"
                 )

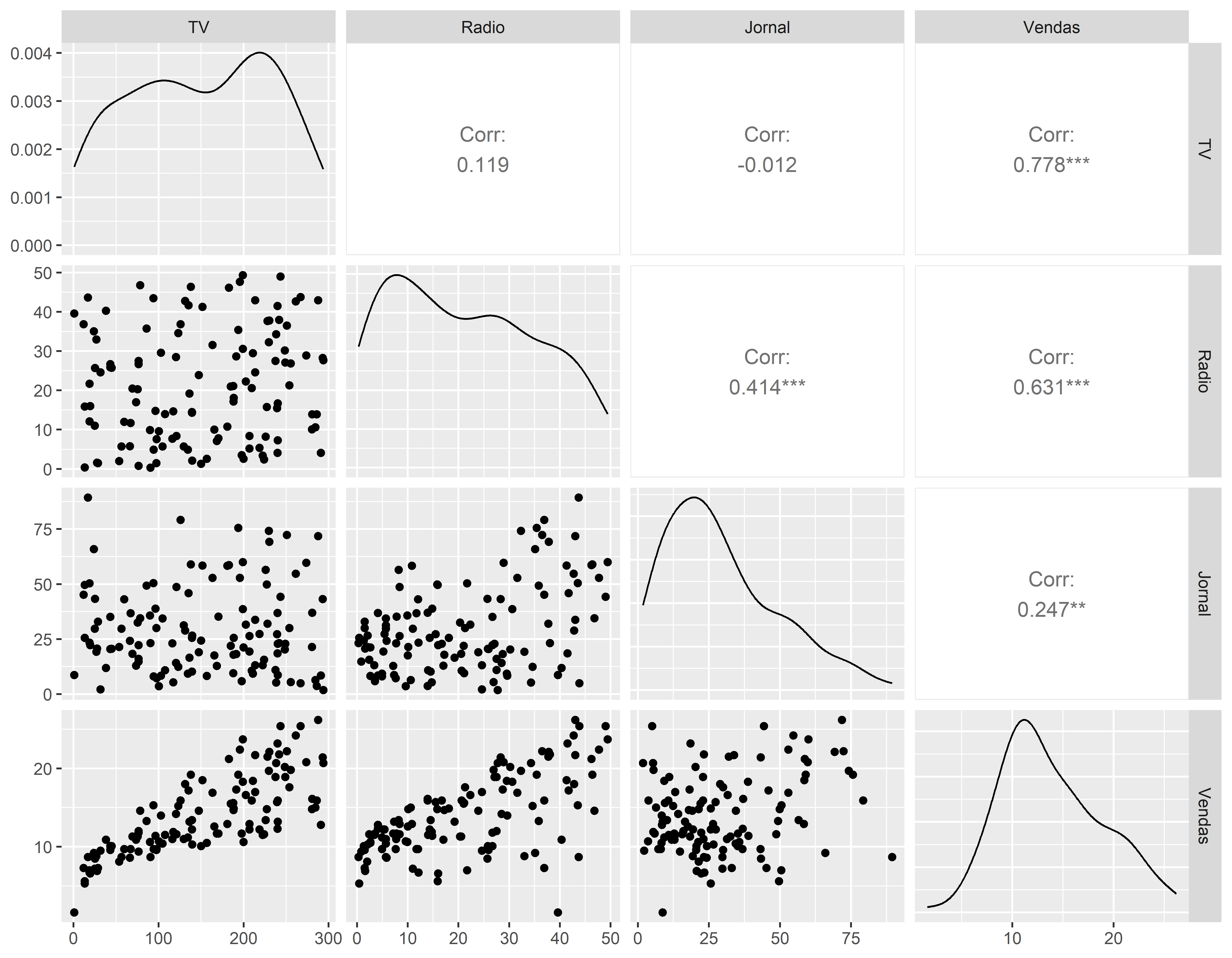
Matriz de dispersão

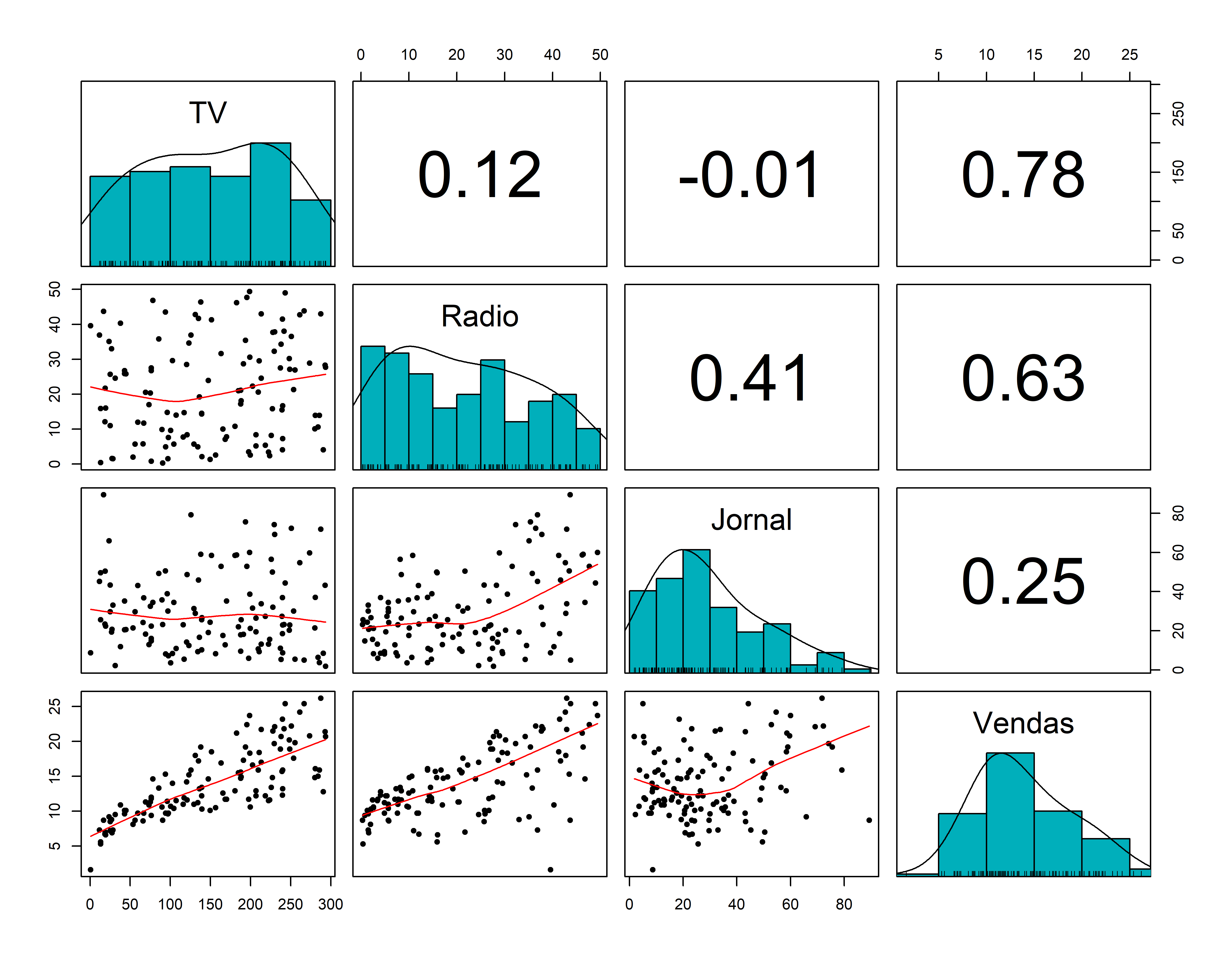
library(psych)
pairs.panels(conj_treino, 
             method = "pearson", # metodo de correlação
             hist.col = "#00AFBB",
             density = TRUE,  # mostra graficos de densidade
             ellipses = FALSE # mostra elipses de correlação
             )

Matriz de Correlações

#> corrplot 0.95 loaded
mat_corr <- cor(conj_treino)
corrplot(mat_corr, method = "number", col = "black", cl.pos = "n")

Outra Matriz de Disersão

#> Registered S3 method overwritten by 'GGally':
#>   method from   
#>   +.gg   ggplot2
ggpairs(conj_treino)

1o Mod Regressão

mod1 <- lm( Vendas ~ TV, data = conj_treino)
names(mod1)
#>  [1] "coefficients"  "residuals"     "effects"       "rank"         
#>  [5] "fitted.values" "assign"        "qr"            "df.residual"  
#>  [9] "xlevels"       "call"          "terms"         "model"
coeflinear <- mod1$coefficients[1]
coefang <- mod1$coefficients[2]
summary(mod1)
#> 
#> Call:
#> lm(formula = Vendas ~ TV, data = conj_treino)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -7.6383 -1.9426 -0.0565  1.7033  7.5277 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 6.929269   0.598642   11.57   <2e-16 ***
#> TV          0.046471   0.003471   13.39   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 3.167 on 117 degrees of freedom
#> Multiple R-squared:  0.605,  Adjusted R-squared:  0.6017 
#> F-statistic: 179.2 on 1 and 117 DF,  p-value: < 2.2e-16
ggplot(conj_treino, aes(x=TV, y=Vendas)) +
    geom_point() +
    geom_abline(slope = coefang,intercept = coeflinear, color="blue" ) + 
    geom_hline(yintercept=coeflinear, linetype="dashed", color = "red")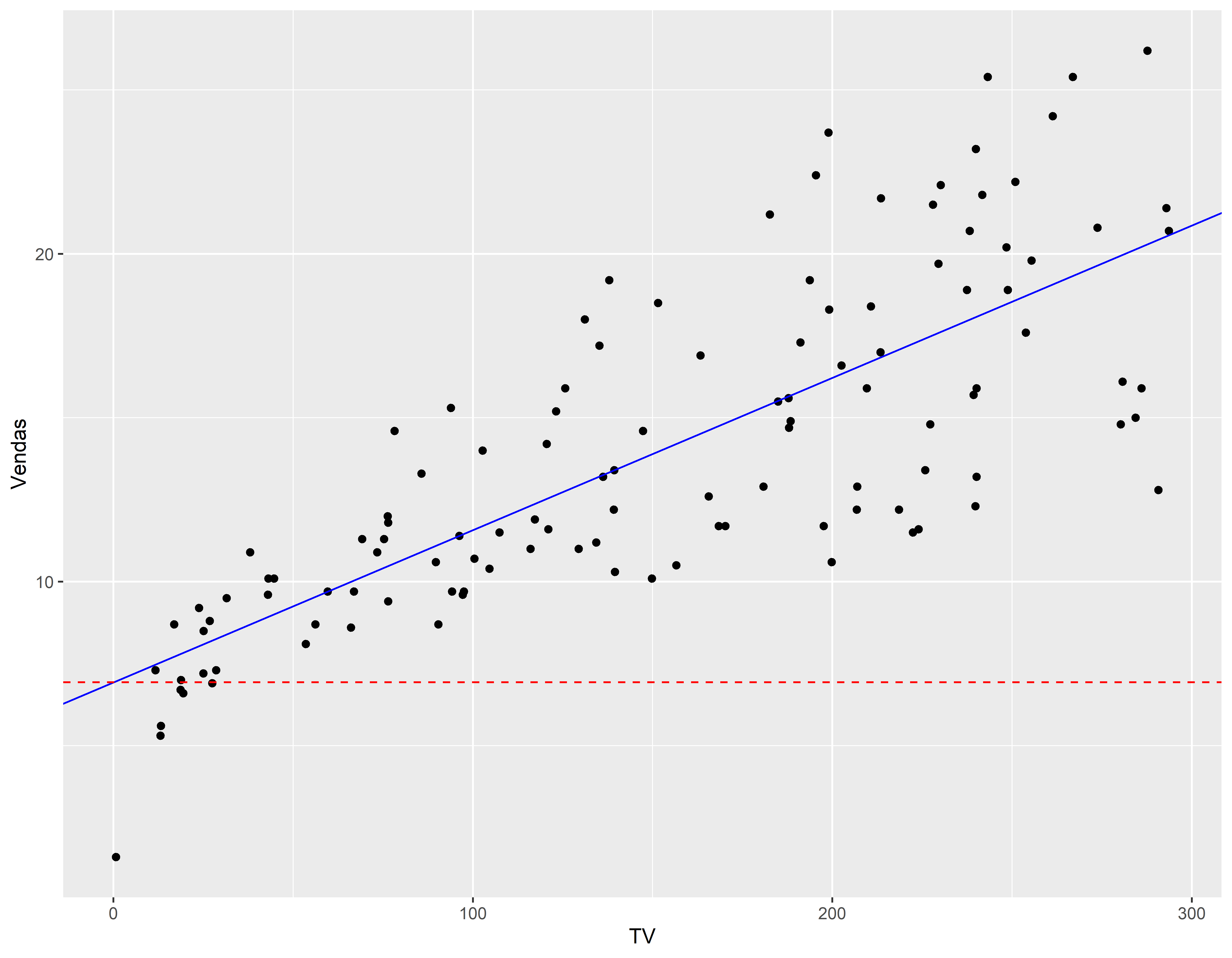

Outra forma de representação do 1o Modelo

library(car)
scatterplot(Vendas ~ TV, data = conj_treino, smooth=F)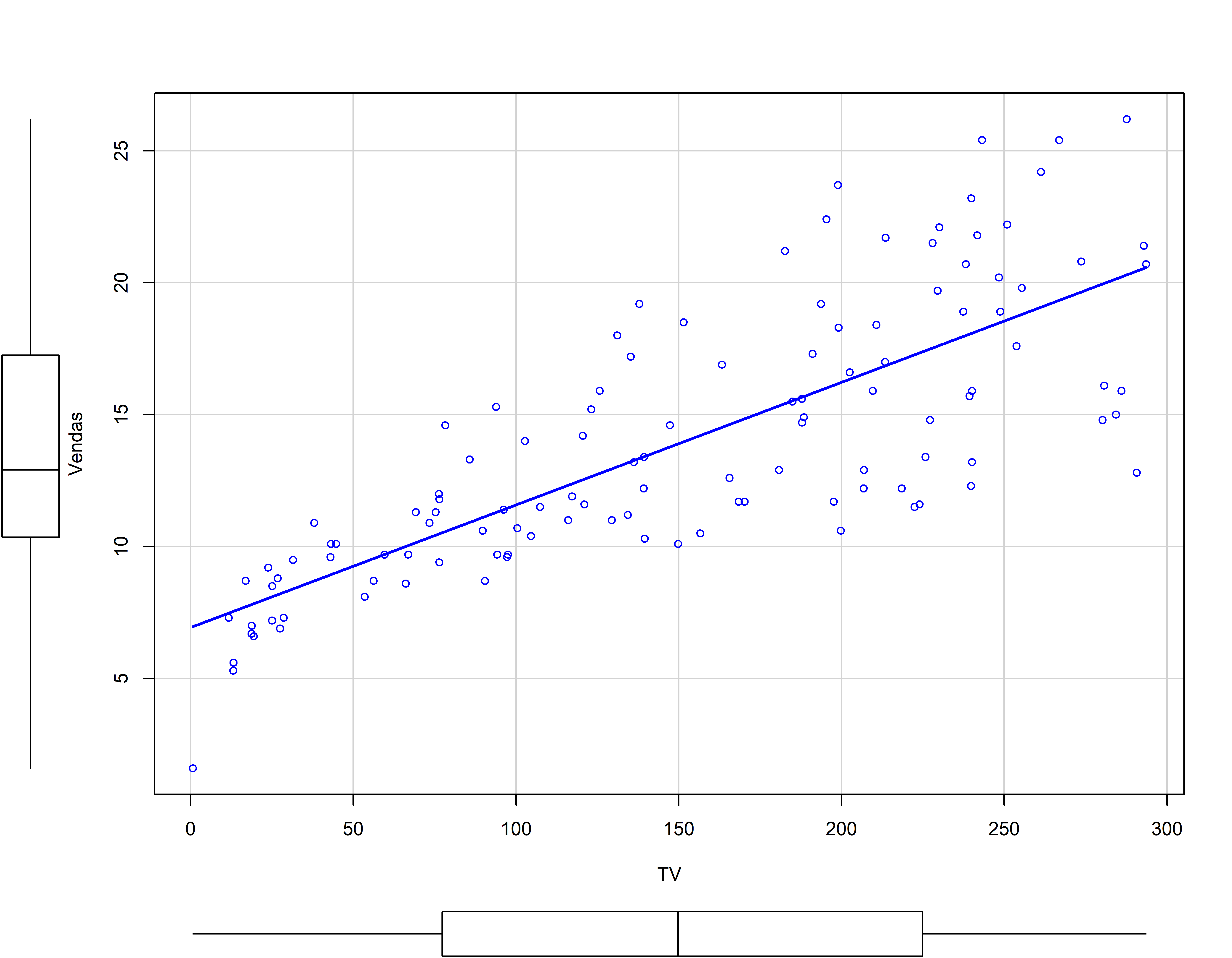

Outra forma de representação do 1o Modelo

#> Registered S3 method overwritten by 'ggside':
#>   method from  
#>   +.gg   GGally
ggplot(conj_treino, aes(x=TV, y=Vendas)) +
    geom_point() +
    geom_smooth(method = lm, se = FALSE) + 
    geom_xsidehistogram(bins = round(1+3.322*log10(nrow(conj_treino)),0)) + 
    geom_ysidehistogram(bins = round(1+3.322*log10(nrow(conj_treino)),0))  
#> `geom_smooth()` using formula = 'y ~ x'
#> Warning: `is.ggproto()` was deprecated in ggplot2 3.5.2.
#> ℹ Please use `is_ggproto()` instead.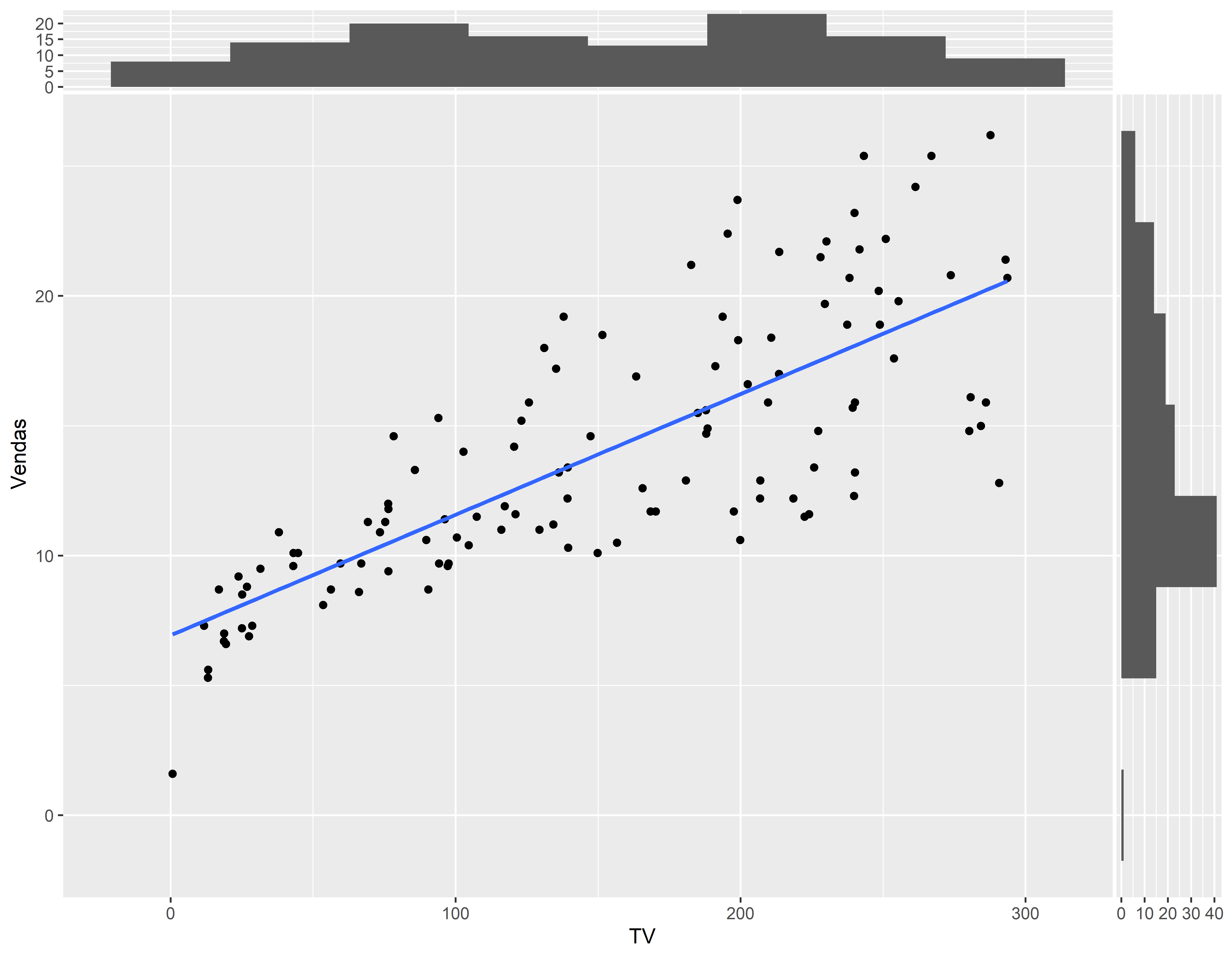

Extraindo informações do 1o ajuste

summary(mod1)$sigma
#> [1] 3.167319
summary(mod1)$r.squared
#> [1] 0.605027

Extraindo usando uma função do pacote car

brief(mod1)
#>            (Intercept)      TV
#> Estimate         6.929 0.04647
#> Std. Error       0.599 0.00347
#> 
#>  Residual SD = 3.17 on 117 df, R-squared = 0.605

Intervalo de Confiança

summary(mod1)
#> 
#> Call:
#> lm(formula = Vendas ~ TV, data = conj_treino)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -7.6383 -1.9426 -0.0565  1.7033  7.5277 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 6.929269   0.598642   11.57   <2e-16 ***
#> TV          0.046471   0.003471   13.39   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 3.167 on 117 degrees of freedom
#> Multiple R-squared:  0.605,  Adjusted R-squared:  0.6017 
#> F-statistic: 179.2 on 1 and 117 DF,  p-value: < 2.2e-16
confint(mod1)
#>                  2.5 %     97.5 %
#> (Intercept) 5.74368904 8.11484821
#> TV          0.03959625 0.05334545

Anova

anova(mod1)
#> Analysis of Variance Table
#> 
#> Response: Vendas
#>            Df Sum Sq Mean Sq F value    Pr(>F)    
#> TV          1 1798.0 1797.95  179.22 < 2.2e-16 ***
#> Residuals 117 1173.7   10.03                      
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Previsões

#?predict
predict(mod1, data.frame(TV=c(50, 150, 250)), interval = "prediction")
#>         fit       lwr      upr
#> 1  9.252811  2.915787 15.58983
#> 2 13.899896  7.600884 20.19891
#> 3 18.546982 12.211175 24.88279

Calculando o erro padrão do resíduo com amostra de teste

##Erro com conjunto de teste
sqrt(mean((conj_teste$Vendas - predict(mod1, conj_teste)) ^ 2)) 
#> [1] 3.41382
## Error com conjunto de treino
summary(mod1)$sigma
#> [1] 3.167319

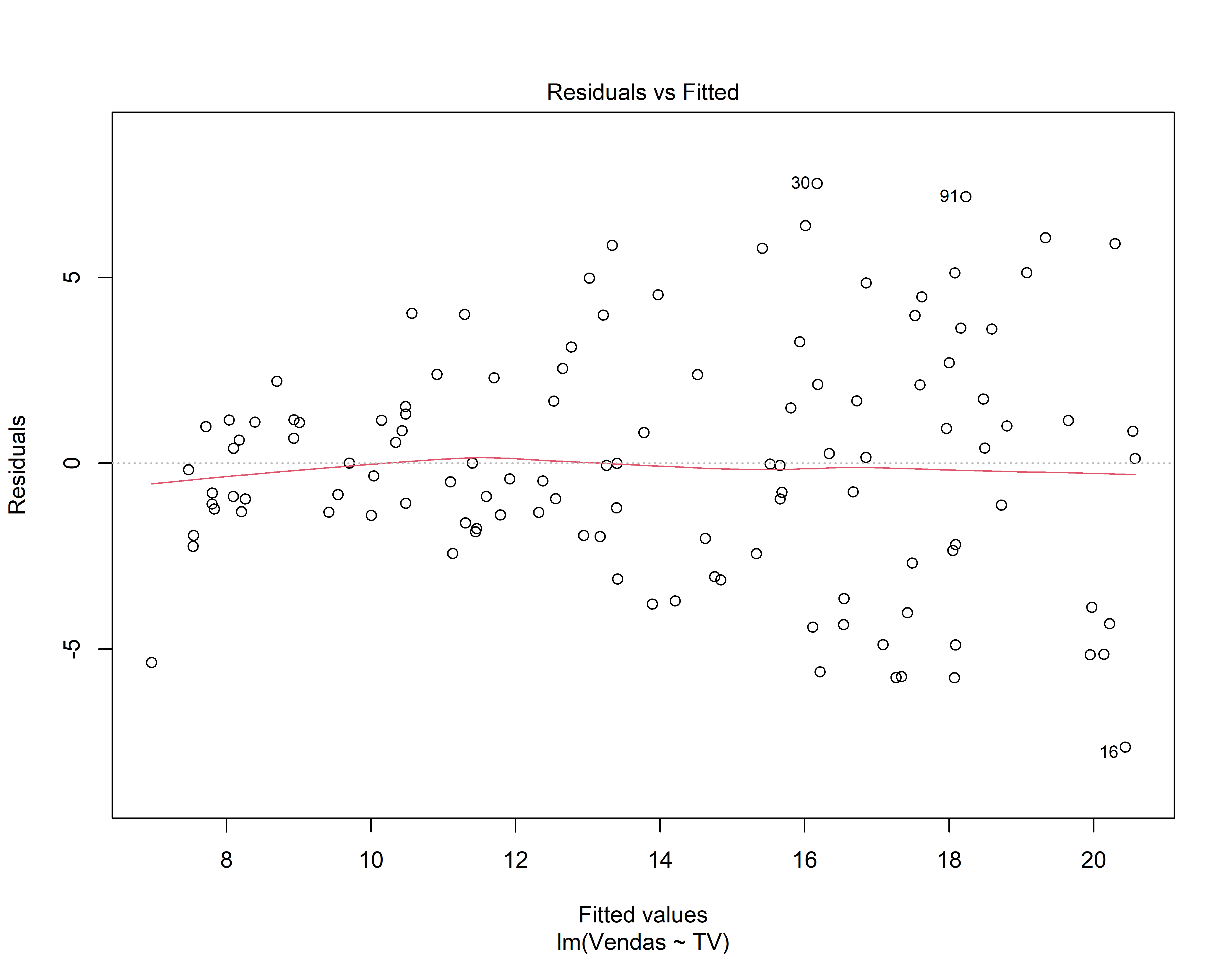
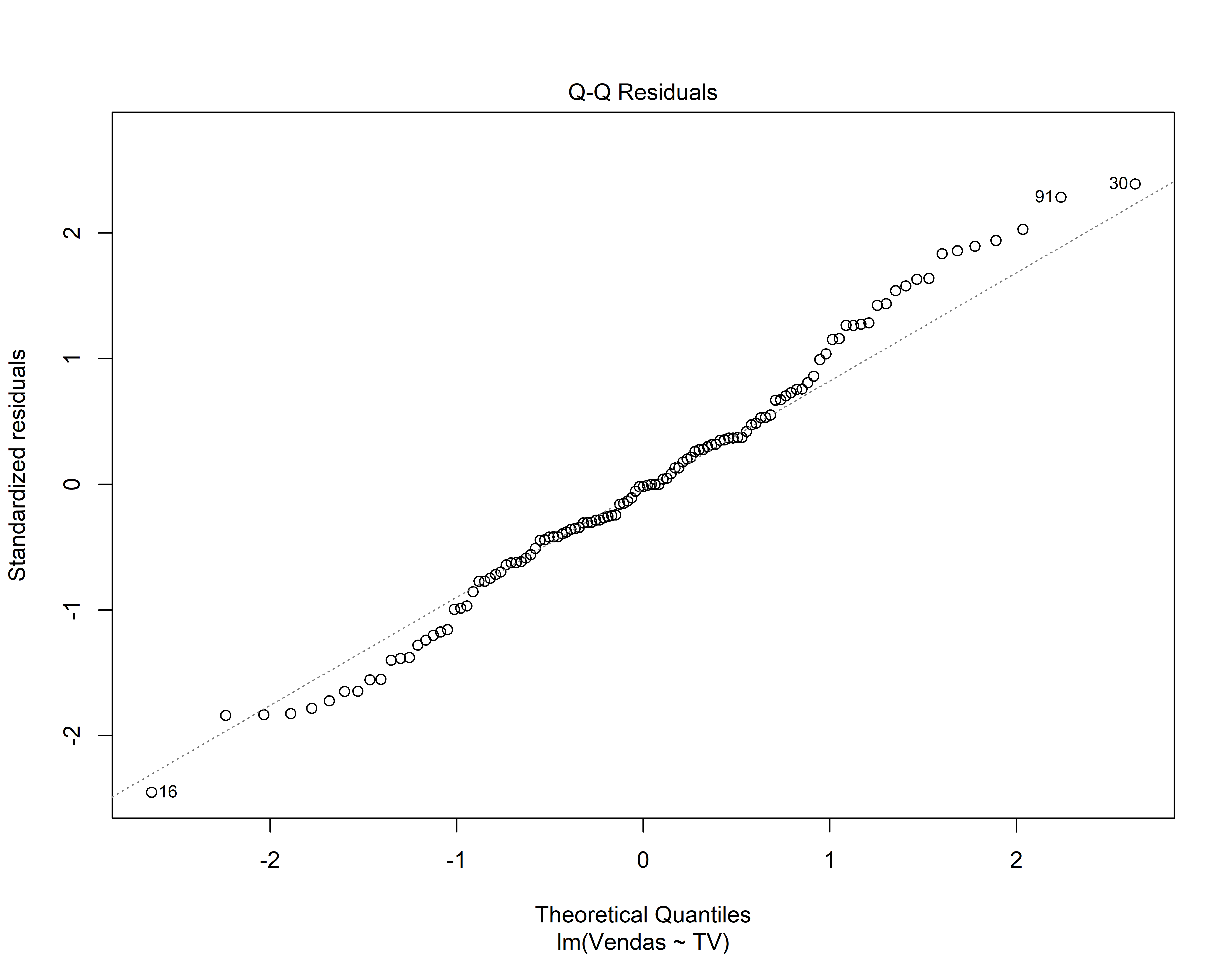
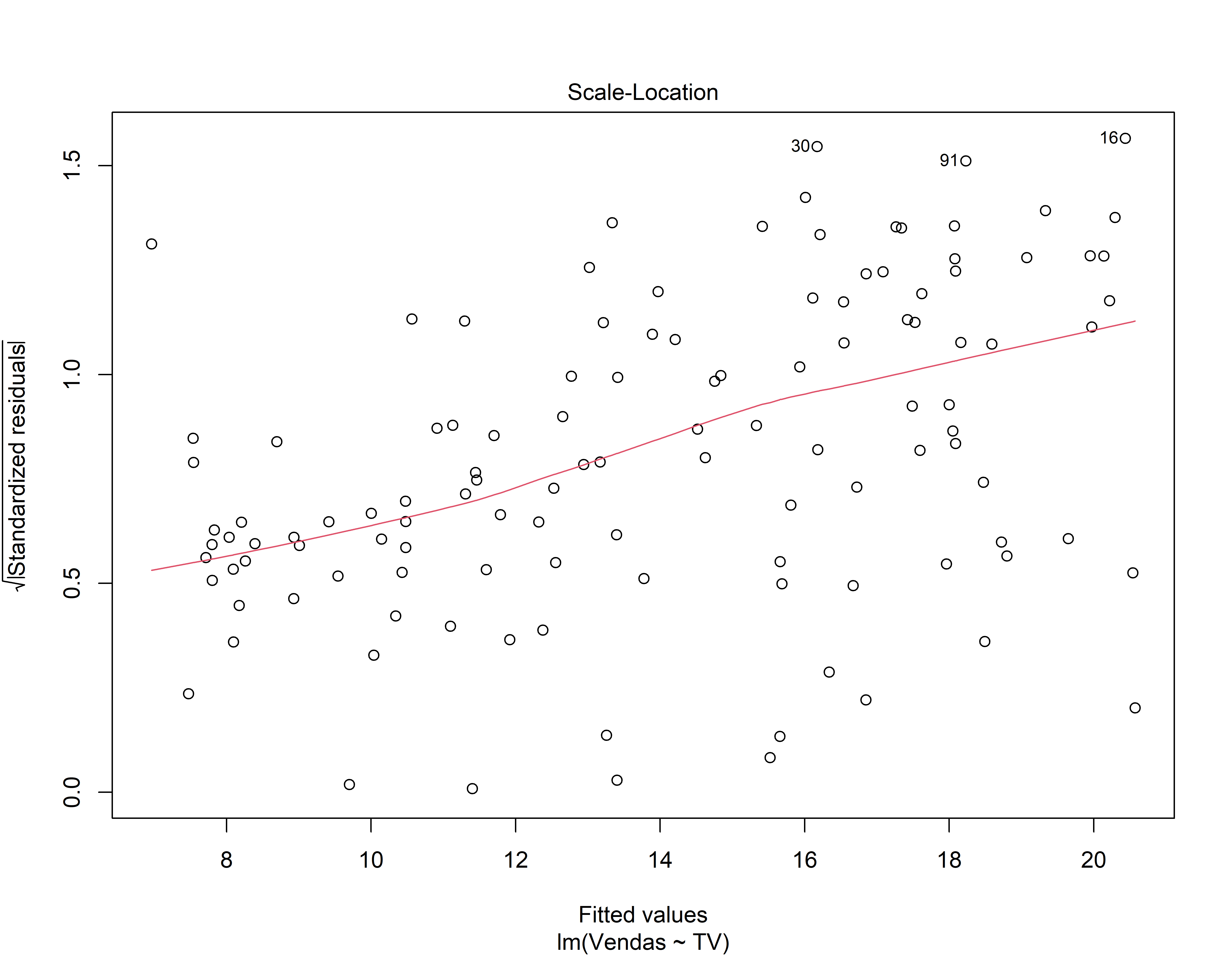
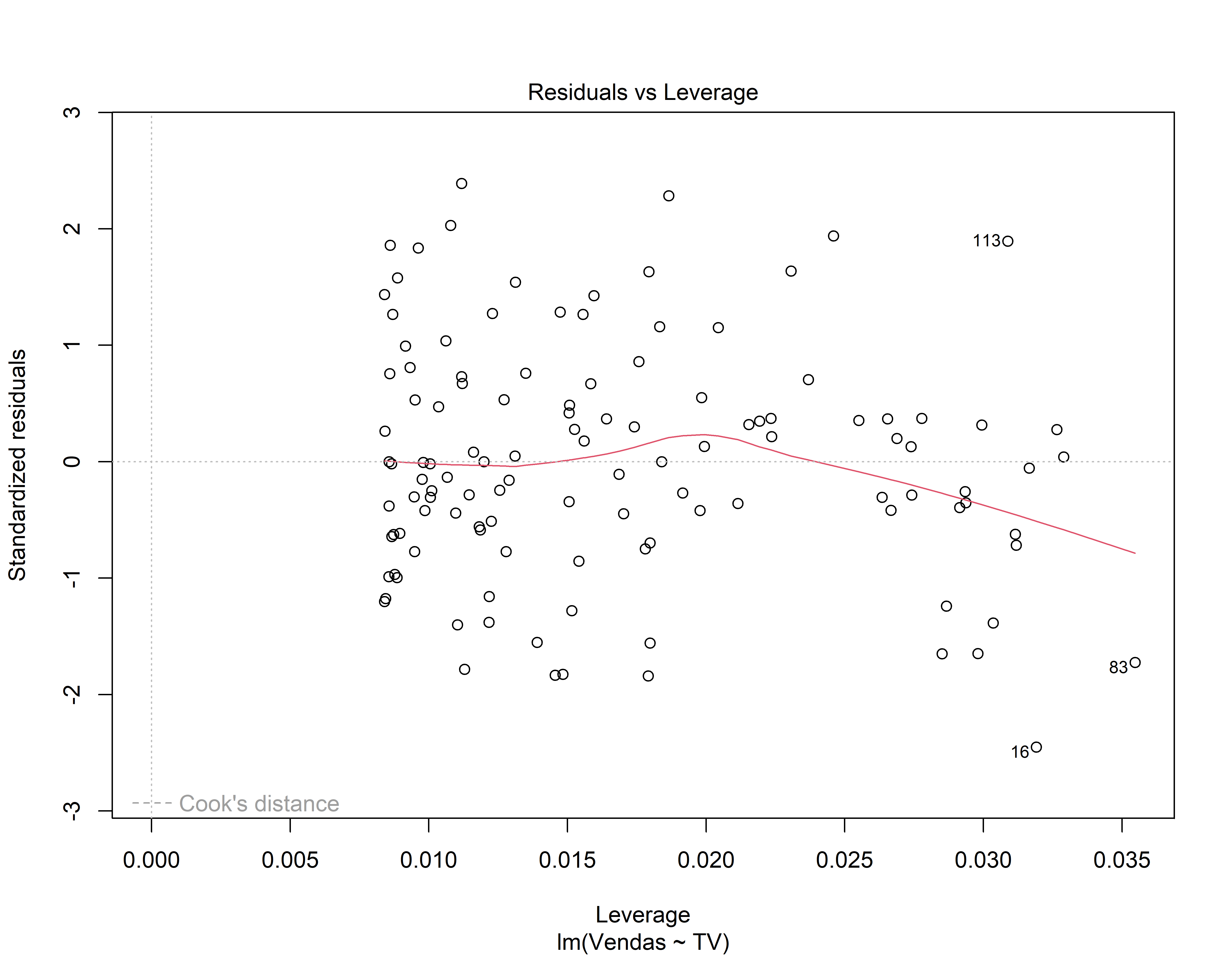
Análise dos resíduos do 1o modelo

plot(mod1)

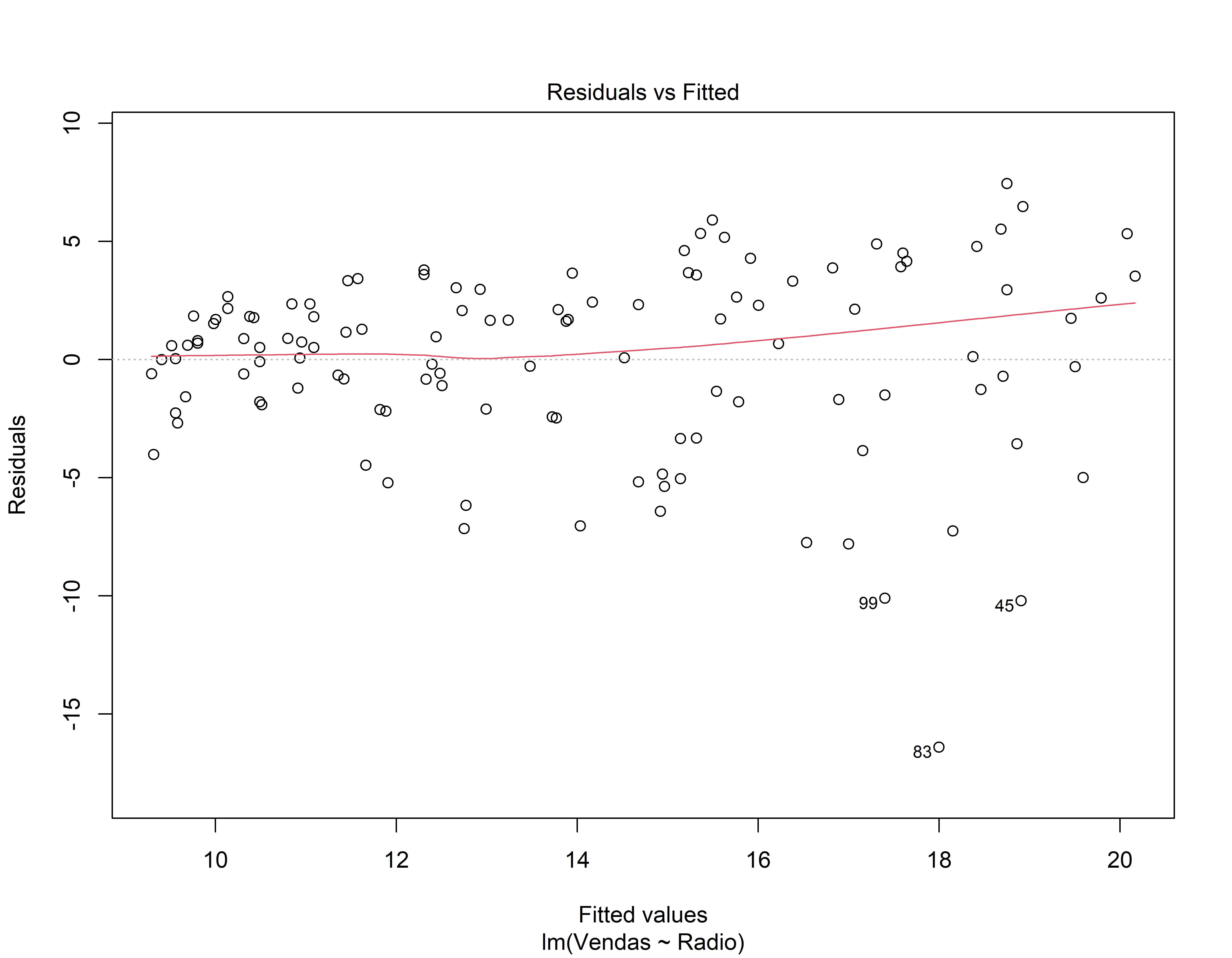
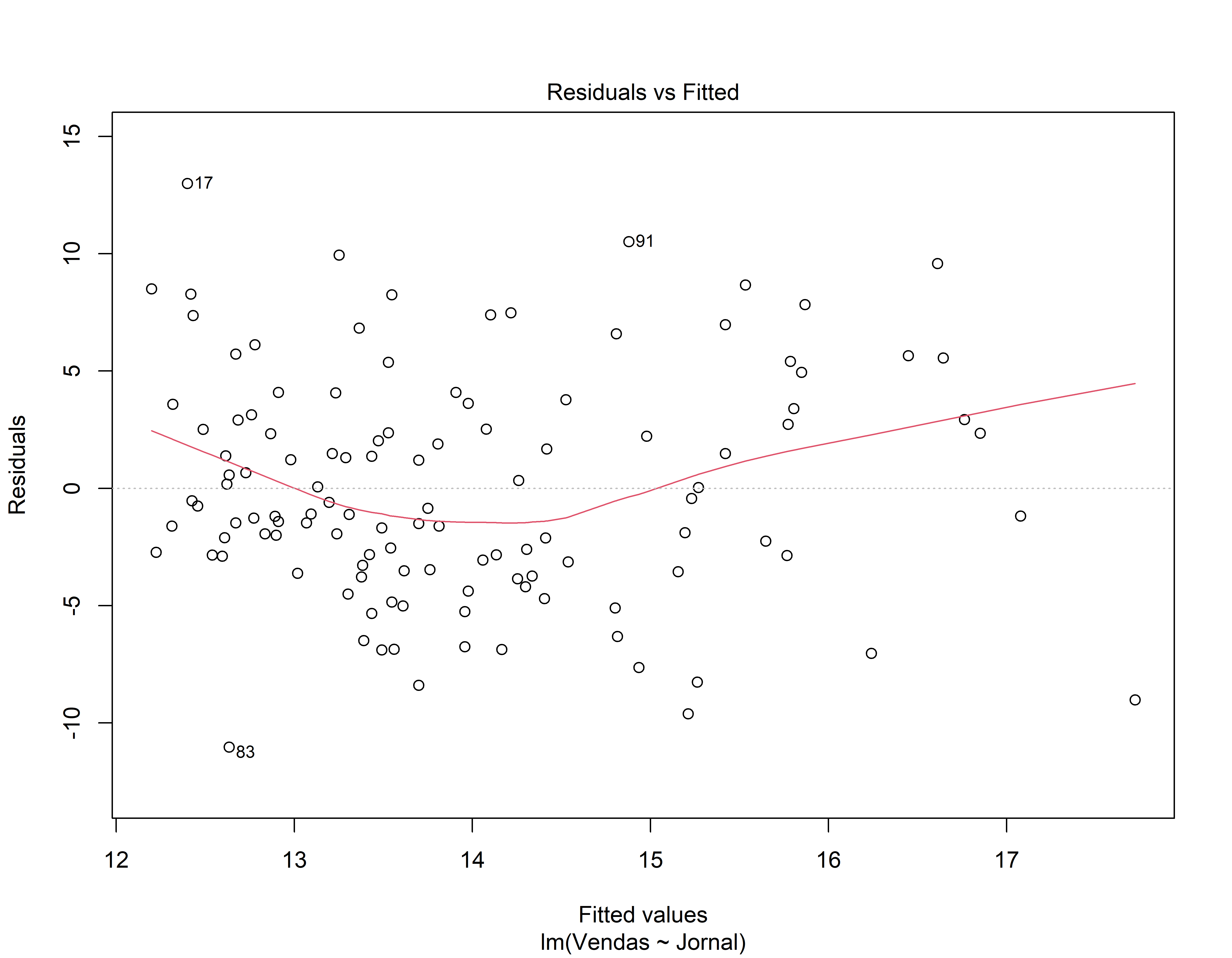
  • Gráfico de Resíduos vs valor ajustado (fitted): Os resíduos estão igualmente espalhados em torno de uma linha horizontal sem padrões distintos? (isso é uma boa indicação de que você não tem relações não lineares)
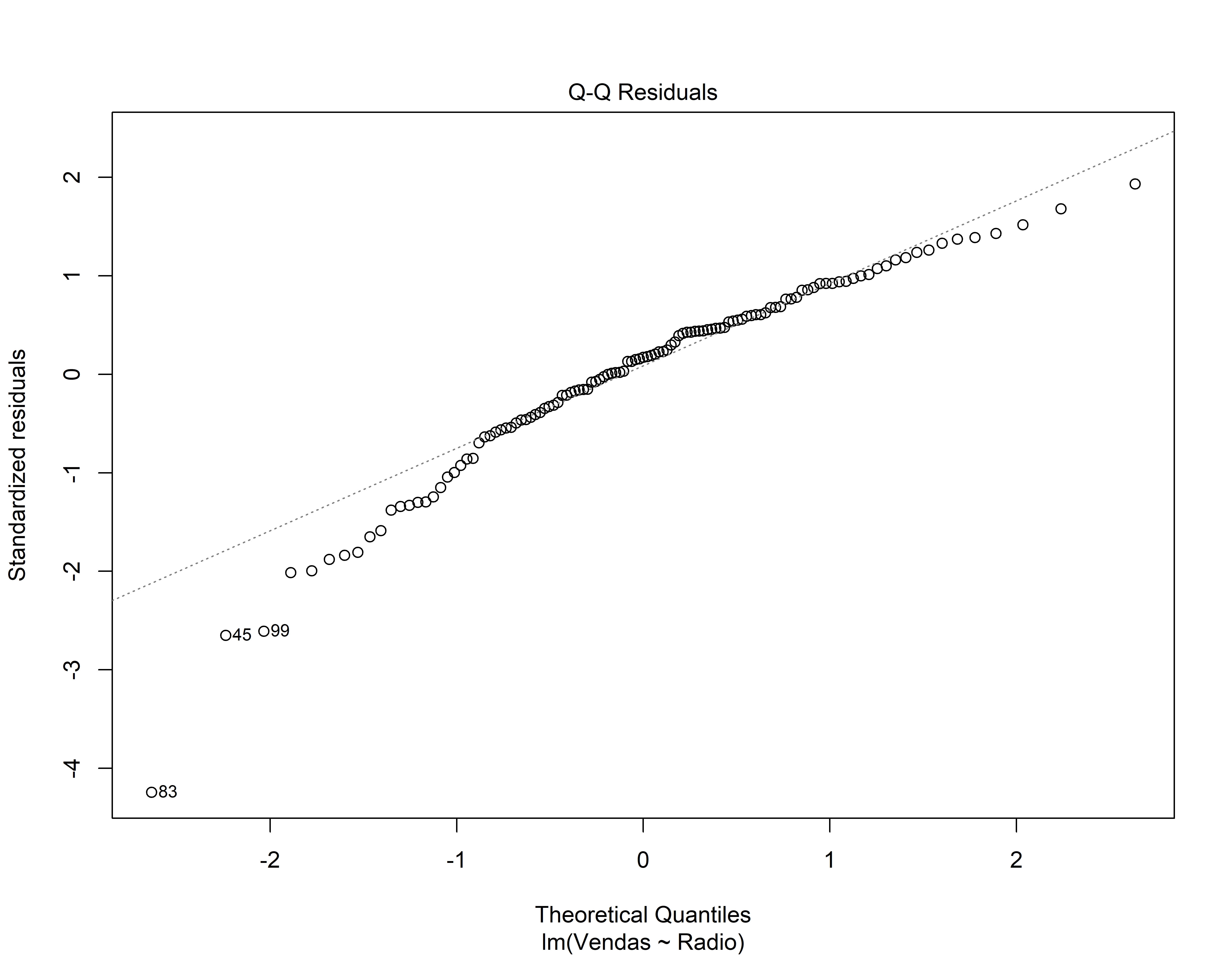
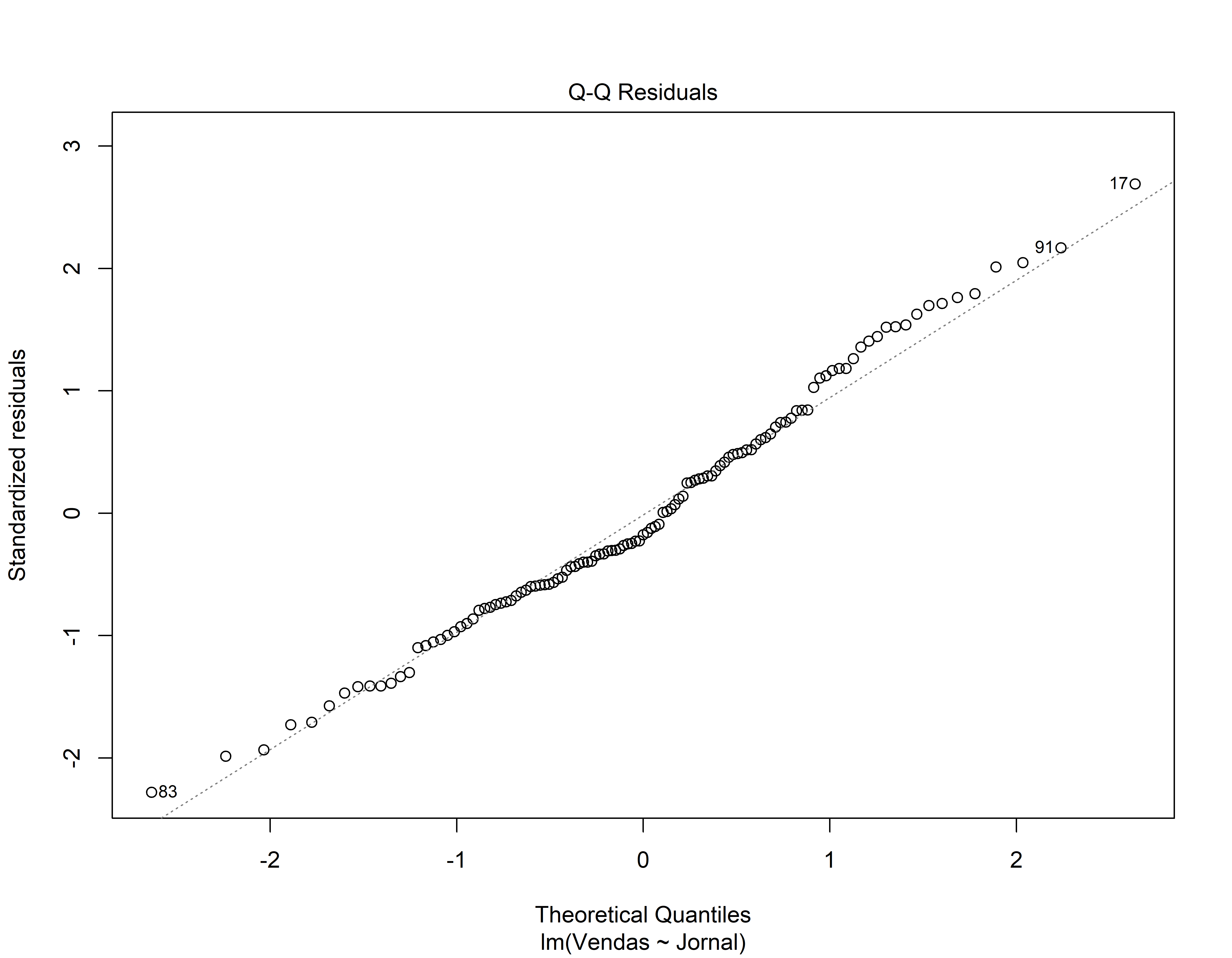
  • Gráfico de quantis normais (Normal QQ). Os resíduos seguem bem a linha reta ou se desviam severamente? (isso é uma indicação que os resíduos se distribuem como a normal)
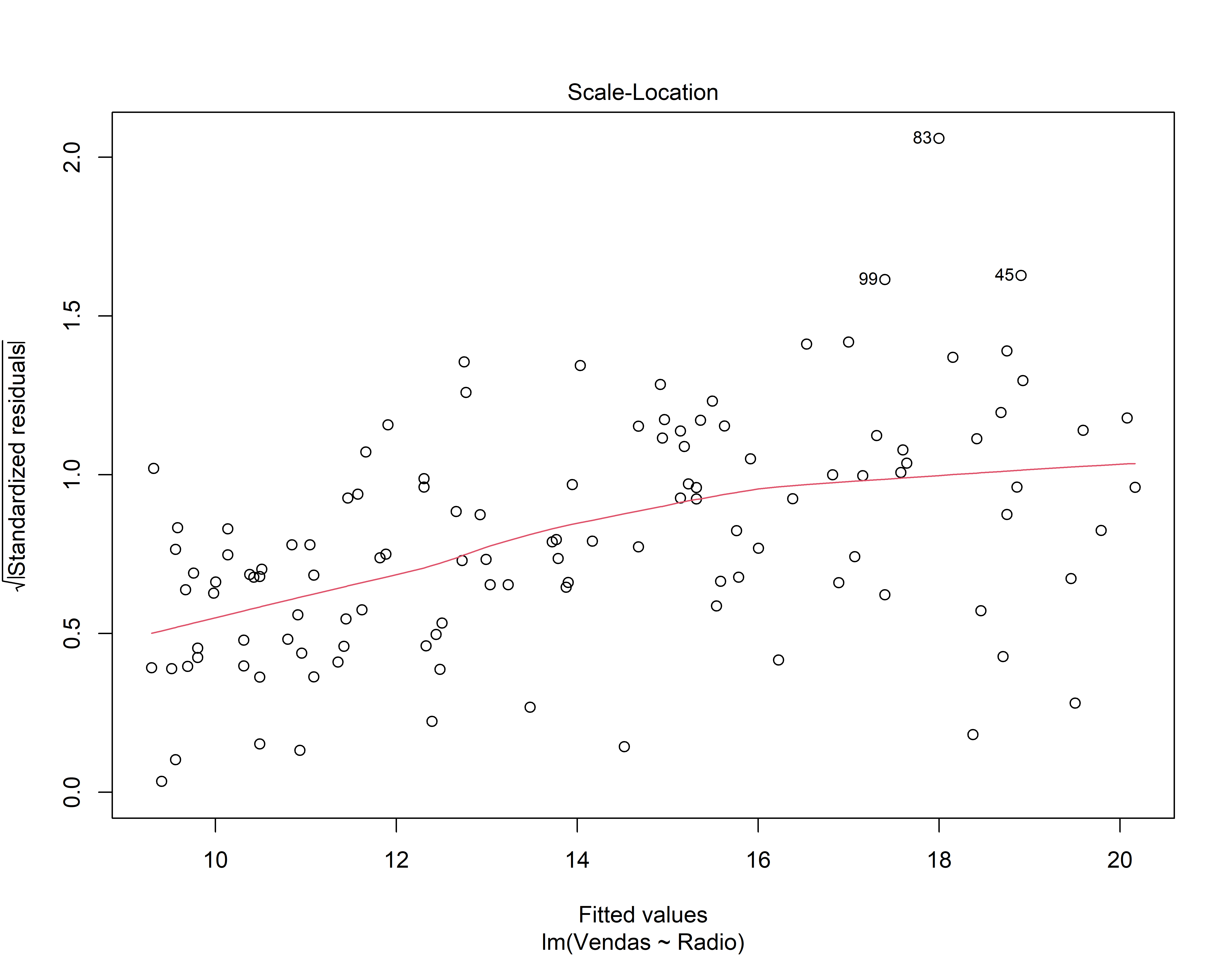
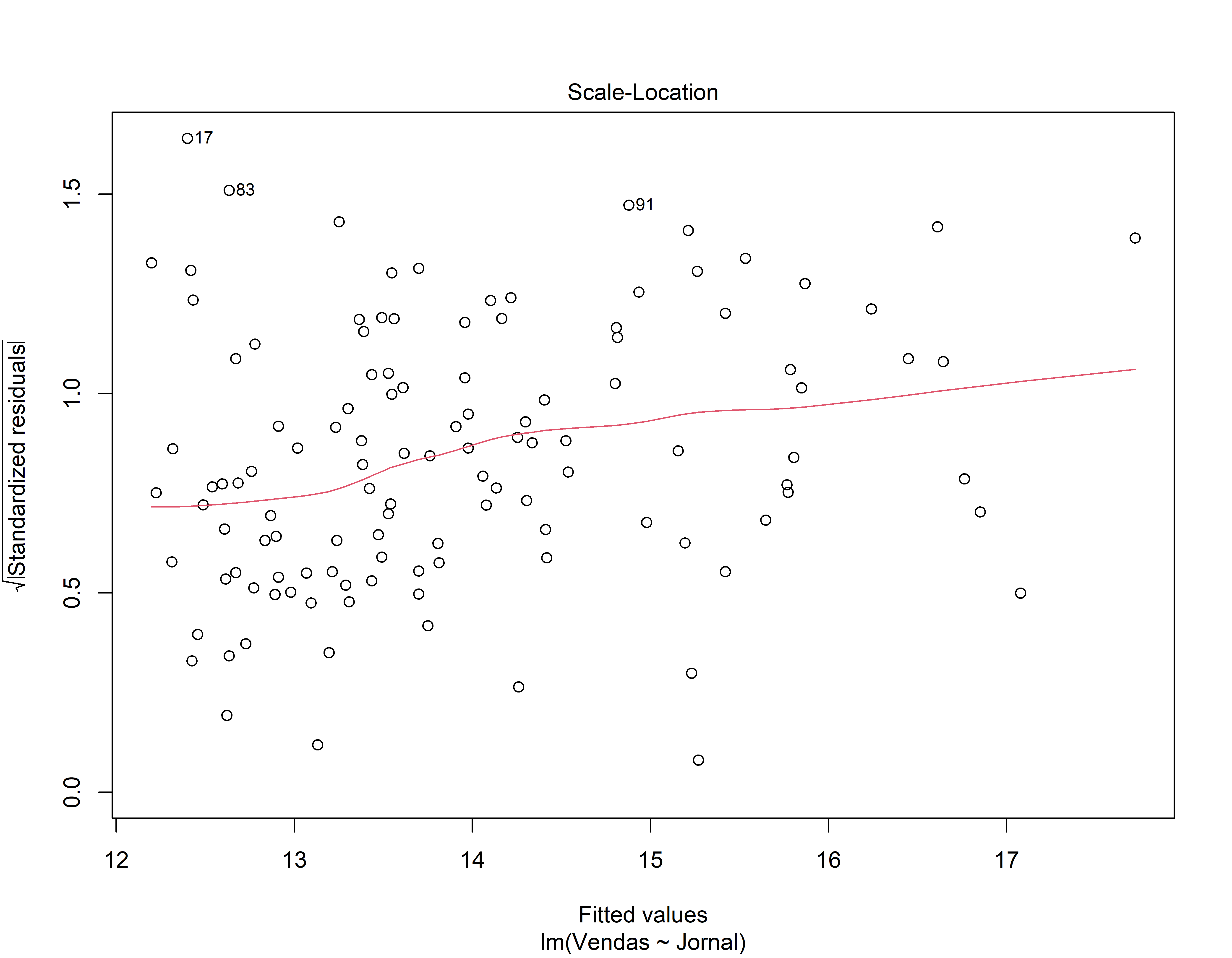
  • Gráfico de Dispersão-Localização. Você está vendo uma linha horizontal com pontos espalhados aleatoriamente ao longo dela? (Isto indica que a variância é constante)
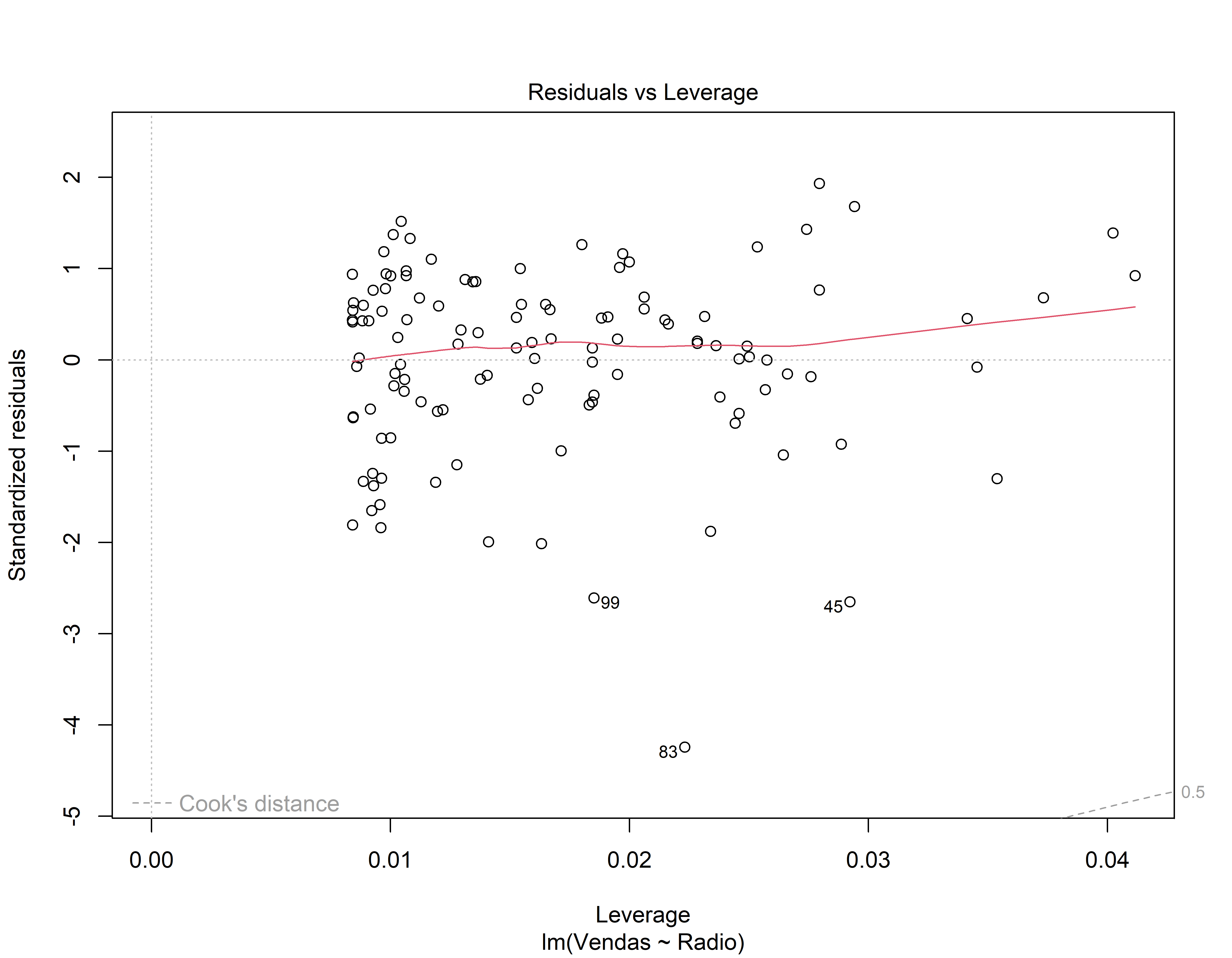
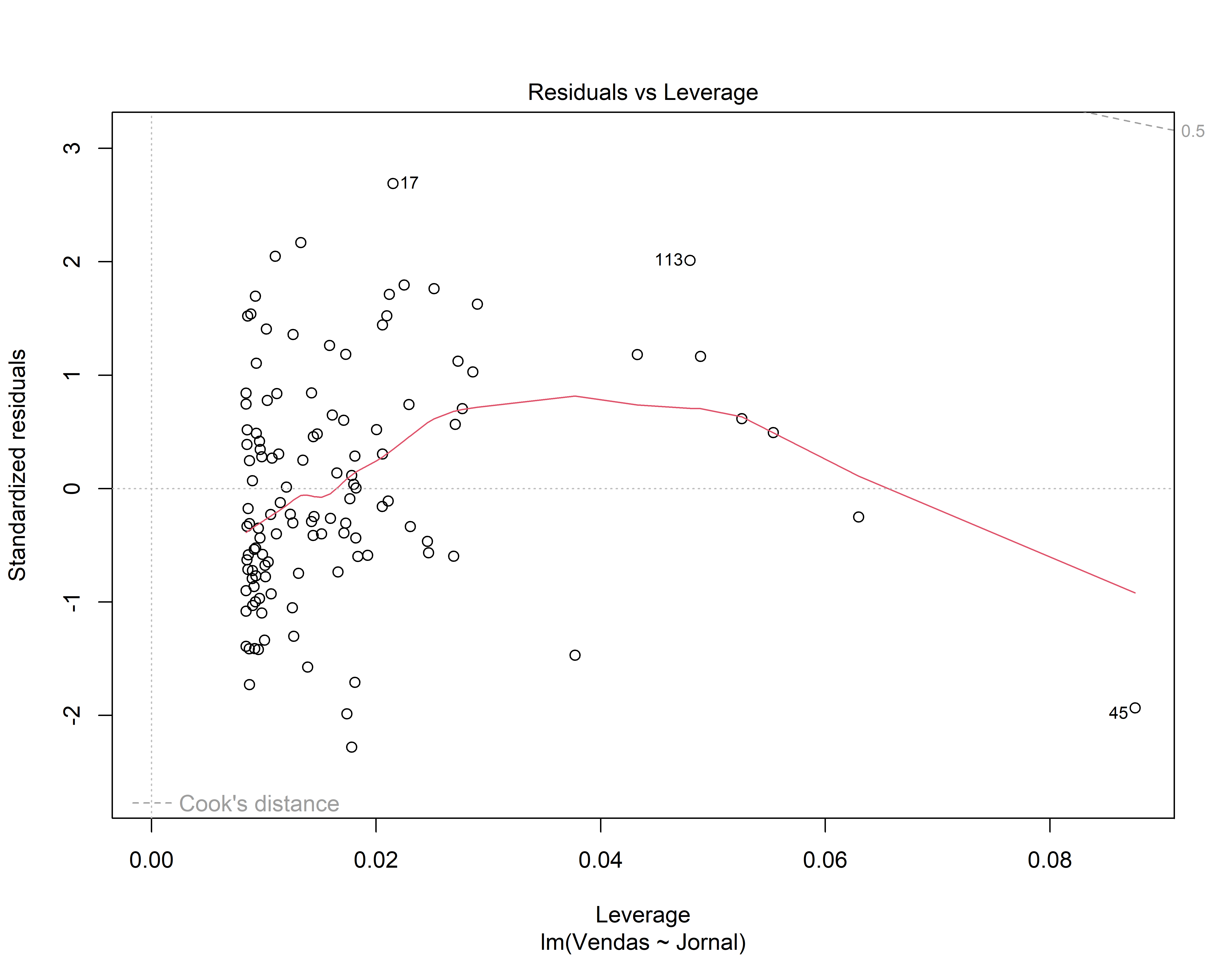
  • Gráfico de Resíduos vs influência (leverage). A distância de Cook tem valor alto? ( isto indica que o dado tem influência para os resultados obtidos na regressão)

Outros testes

Teste de normalidade Teste de heterocedasticidade (Bresch-Pagan) Teste de autocorrelação (Durbin-Watson)

library(lmtest)
#> Carregando pacotes exigidos: zoo
#> 
#> Anexando pacote: 'zoo'
#> Os seguintes objetos são mascarados por 'package:base':
#> 
#>     as.Date, as.Date.numeric
mod1_sum <- summary(mod1)
# Teste de normalidade
shapiro.test(mod1_sum$residuals)
#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  mod1_sum$residuals
#> W = 0.98867, p-value = 0.4293
# Teste de hetrocedasticidade
bptest(mod1)
#> 
#>  studentized Breusch-Pagan test
#> 
#> data:  mod1
#> BP = 24.654, df = 1, p-value = 6.86e-07
# Teste de autocorrelação
dwtest(mod1)
#> 
#>  Durbin-Watson test
#> 
#> data:  mod1
#> DW = 2.0232, p-value = 0.5506
#> alternative hypothesis: true autocorrelation is greater than 0

2o Modelo de Regressão

mod2 <- lm( Vendas ~ Radio, data = conj_treino)
coeflinear <- mod2$coefficients[1]
coefang <- mod2$coefficients[2]
summary(mod2)
#> 
#> Call:
#> lm(formula = Vendas ~ Radio, data = conj_treino)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -16.396  -1.851   0.675   2.522   7.451 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  9.22746    0.64377  14.333  < 2e-16 ***
#> Radio        0.22144    0.02515   8.806 1.38e-14 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 3.908 on 117 degrees of freedom
#> Multiple R-squared:  0.3986, Adjusted R-squared:  0.3935 
#> F-statistic: 77.55 on 1 and 117 DF,  p-value: 1.384e-14
ggplot(propaganda, aes(x=Radio, y=Vendas)) +
    geom_point() +
    geom_abline(slope = coefang,intercept = coeflinear, color="blue" ) + 
    geom_hline(yintercept=coeflinear, linetype="dashed", color = "red")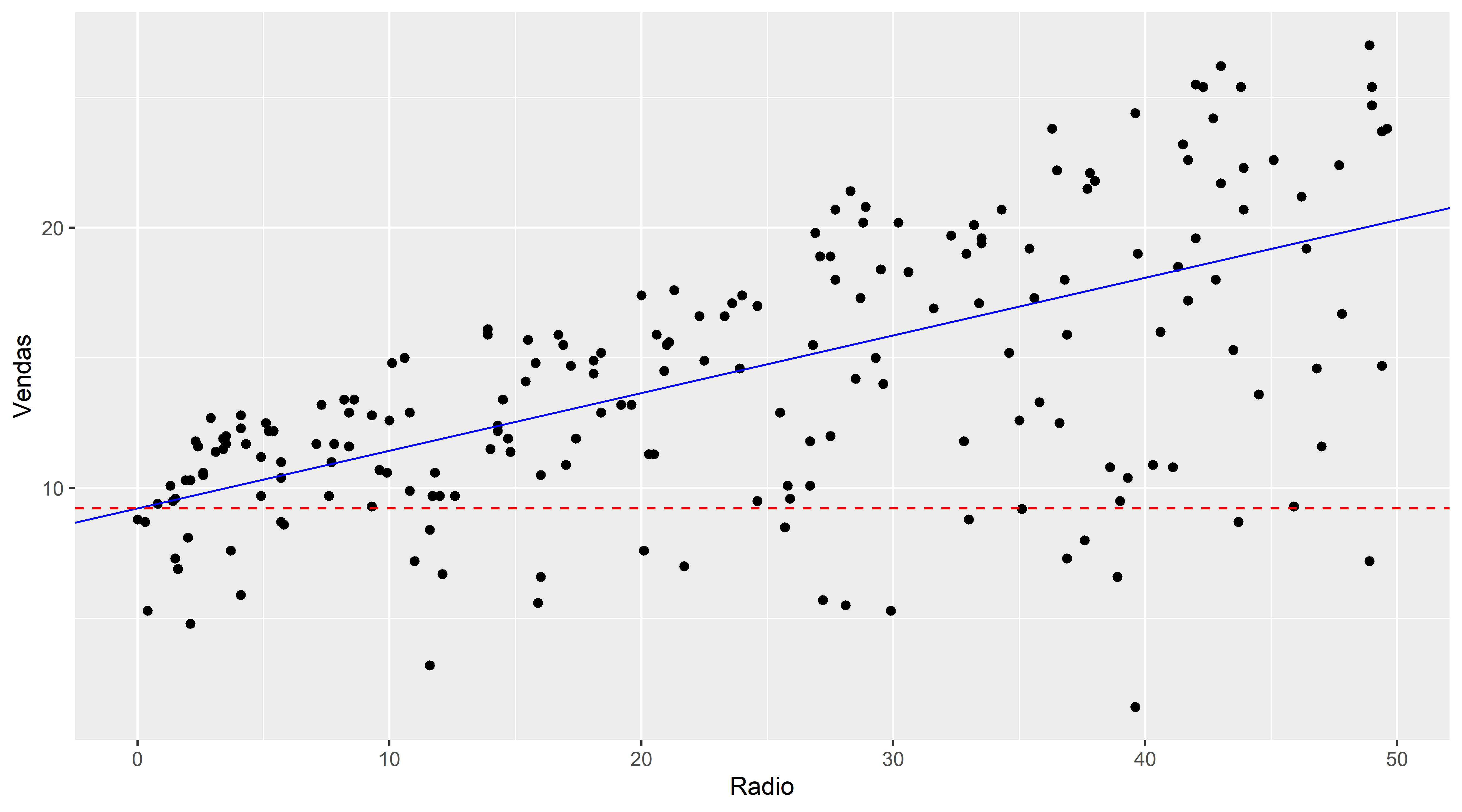

Outra forma de representação do 2o Modelo

scatterplot(Vendas ~ Radio, data = conj_treino, smooth=F)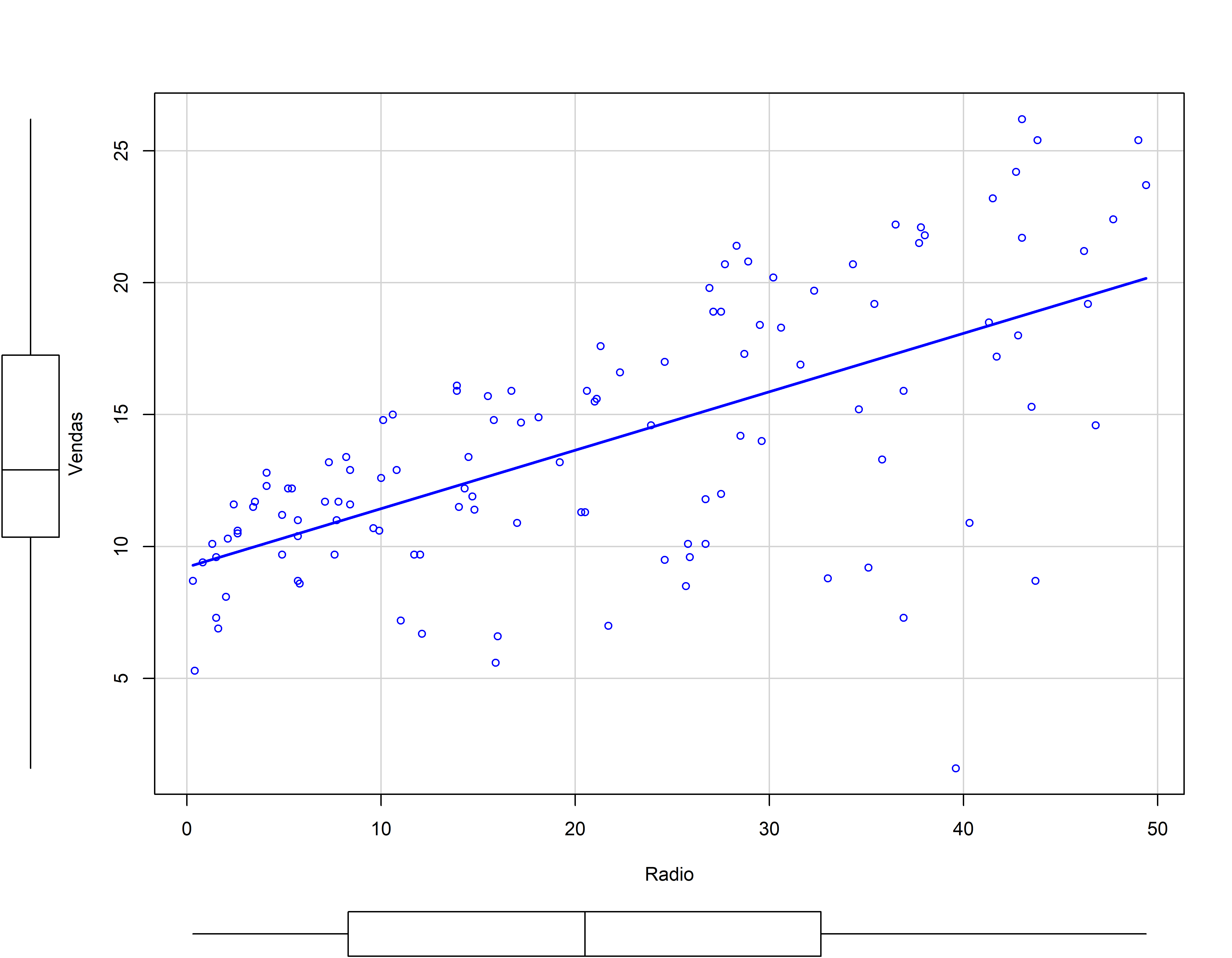

Calculando o erro padrão do resíduo com amostra de teste

## Erro com conjunto de teste
sqrt(mean((conj_teste$Vendas - predict(mod2, conj_teste)) ^ 2)) 
#> [1] 4.808117
## Error com conjunto de treino
summary(mod2)$sigma
#> [1] 3.908233

Análise dos resíduos do 2o modelo

plot(mod2)

3o Modelo de Regressão

mod3 <- lm( Vendas ~ Jornal, data = conj_treino)
coeflinear <- mod3$coefficients[1]
coefang <- mod3$coefficients[2]
summary(mod3)
#> 
#> Call:
#> lm(formula = Vendas ~ Jornal, data = conj_treino)
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -11.0331  -3.2104  -0.8491   3.0389  13.0002 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 12.08457    0.80845  14.948  < 2e-16 ***
#> Jornal       0.06305    0.02290   2.753  0.00685 ** 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 4.884 on 117 degrees of freedom
#> Multiple R-squared:  0.06084,    Adjusted R-squared:  0.05281 
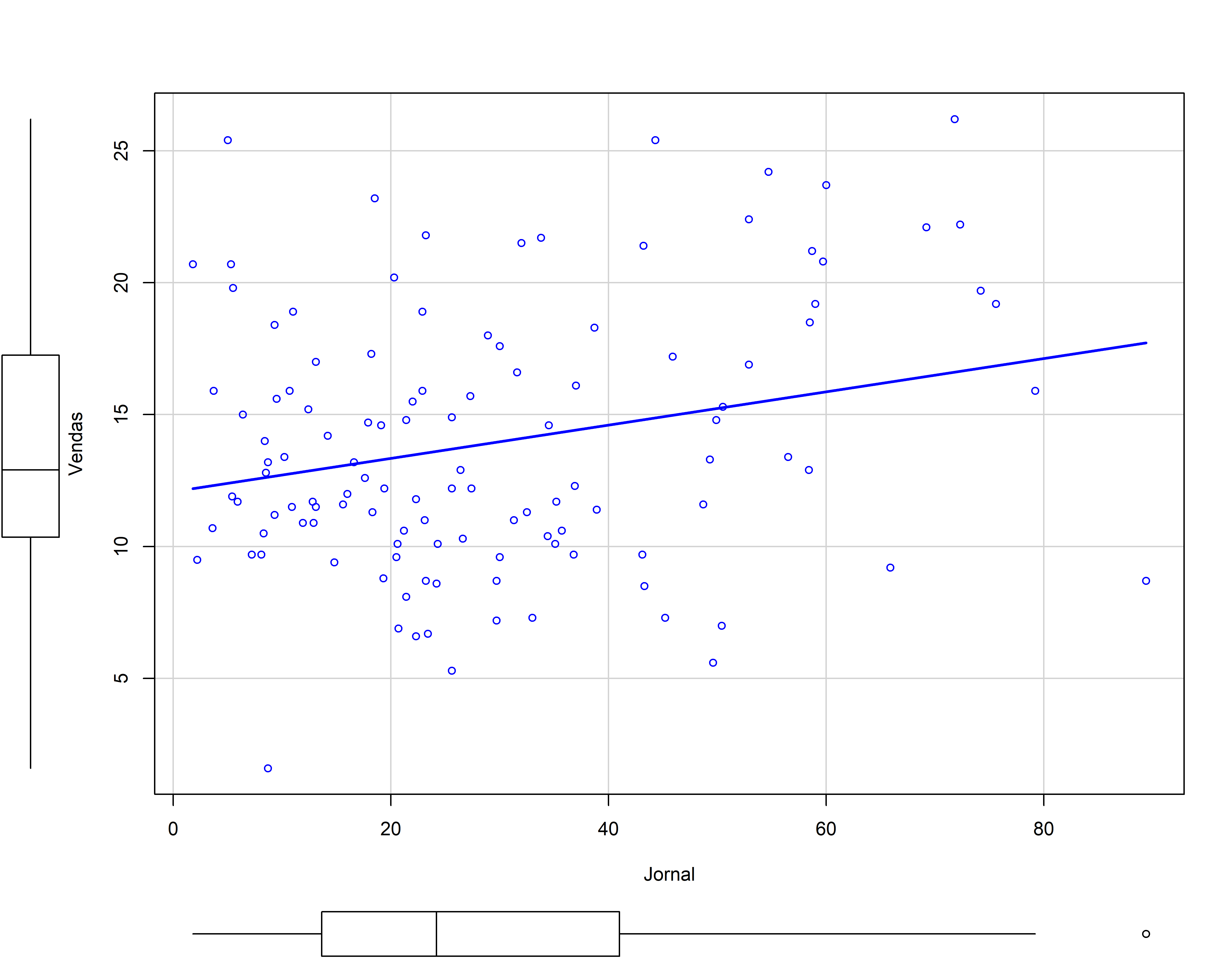
#> F-statistic: 7.579 on 1 and 117 DF,  p-value: 0.006847
ggplot(propaganda, aes(x=Jornal, y=Vendas)) +
    geom_point() +
    geom_abline(slope = coefang,intercept = coeflinear, color="blue" ) + 
    geom_hline(yintercept=coeflinear, linetype="dashed", color = "red")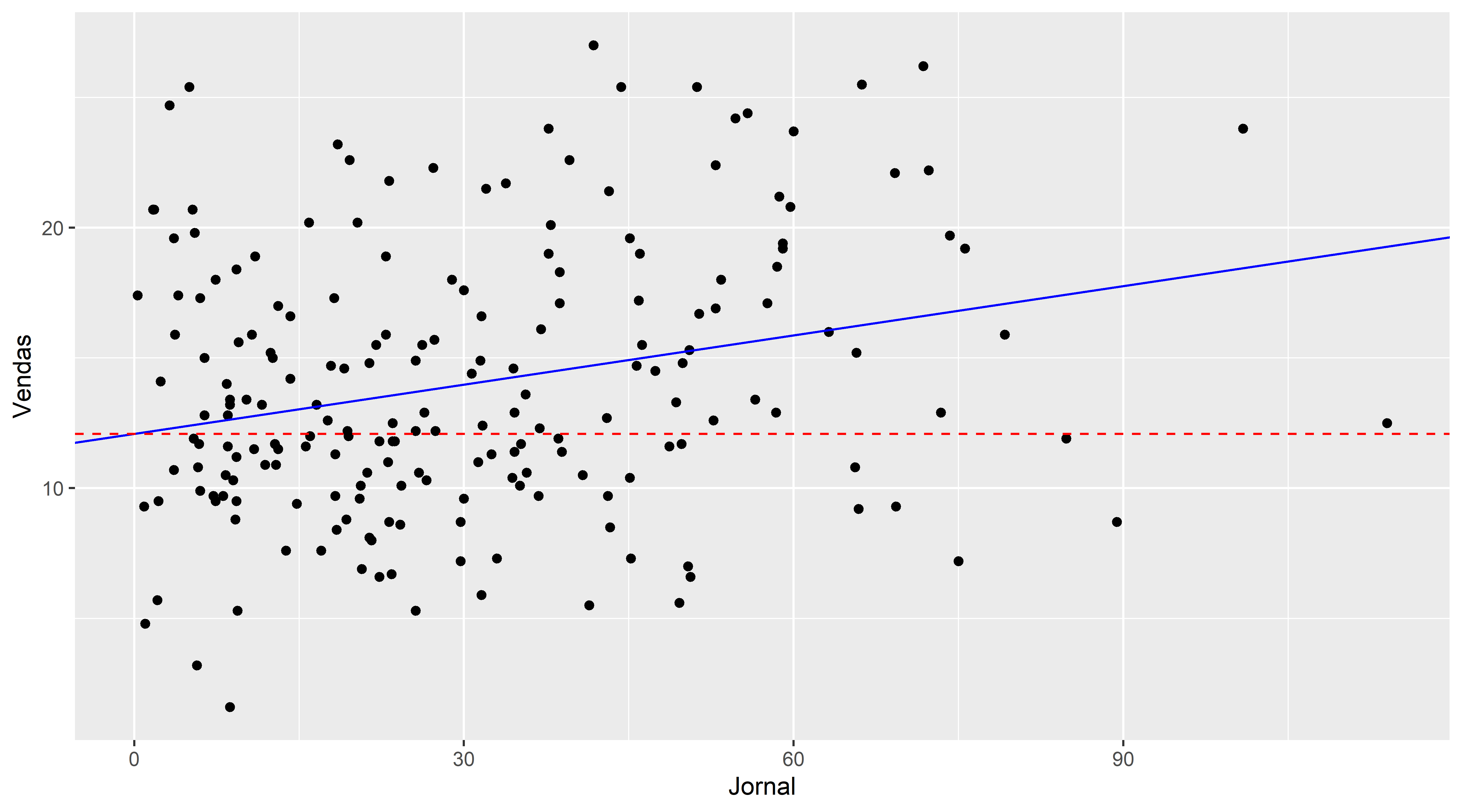

Outra forma de representação do 3o Modelo

scatterplot(Vendas ~ Jornal, data = conj_treino, smooth=F)

Calculando o erro padrão do resíduo com amostra de teste

## Erro com conjunto de teste
sqrt(mean((conj_teste$Vendas - predict(mod3, conj_teste)) ^ 2)) 
#> [1] 5.38693
## Error com conjunto de treino
summary(mod3)$sigma
#> [1] 4.884027

Análise dos resíduos do 3o modelo

plot(mod3)