Arvores de Regressão - Gradient Boosting

Author

Ricardo Accioly

Published

August 20, 2024

Bibliotecas

Avaliando, selecionando dados

data("Boston")
names(Boston)
 [1] "crim"    "zn"      "indus"   "chas"    "nox"     "rm"      "age"    
 [8] "dis"     "rad"     "tax"     "ptratio" "black"   "lstat"   "medv"   
dados <- Boston

Treino e Teste com todas as variáveis

## Vamos criar os conjuntos de treino teste e desenvolver a arvore 
## com todas as variáveis.
library(caret)
set.seed(21)
indice <- createDataPartition(dados$medv, times=1, p=0.75, list=FALSE)
conj_treino <- dados[indice,]
conj_teste <- dados[-indice,]
head(conj_treino)
     crim   zn indus chas   nox    rm  age    dis rad tax ptratio  black lstat
1 0.00632 18.0  2.31    0 0.538 6.575 65.2 4.0900   1 296    15.3 396.90  4.98
3 0.02729  0.0  7.07    0 0.469 7.185 61.1 4.9671   2 242    17.8 392.83  4.03
4 0.03237  0.0  2.18    0 0.458 6.998 45.8 6.0622   3 222    18.7 394.63  2.94
5 0.06905  0.0  2.18    0 0.458 7.147 54.2 6.0622   3 222    18.7 396.90  5.33
6 0.02985  0.0  2.18    0 0.458 6.430 58.7 6.0622   3 222    18.7 394.12  5.21
7 0.08829 12.5  7.87    0 0.524 6.012 66.6 5.5605   5 311    15.2 395.60 12.43
  medv
1 24.0
3 34.7
4 33.4
5 36.2
6 28.7
7 22.9
head(conj_teste)
      crim   zn indus chas   nox    rm  age    dis rad tax ptratio  black lstat
2  0.02731  0.0  7.07    0 0.469 6.421 78.9 4.9671   2 242    17.8 396.90  9.14
10 0.17004 12.5  7.87    0 0.524 6.004 85.9 6.5921   5 311    15.2 386.71 17.10
12 0.11747 12.5  7.87    0 0.524 6.009 82.9 6.2267   5 311    15.2 396.90 13.27
16 0.62739  0.0  8.14    0 0.538 5.834 56.5 4.4986   4 307    21.0 395.62  8.47
19 0.80271  0.0  8.14    0 0.538 5.456 36.6 3.7965   4 307    21.0 288.99 11.69
23 1.23247  0.0  8.14    0 0.538 6.142 91.7 3.9769   4 307    21.0 396.90 18.72
   medv
2  21.6
10 18.9
12 18.9
16 19.9
19 20.2
23 15.2

Parametros do GBM

library(gbm)
set.seed(21)
# treinar o modelo GBM
# gbm.fit <- gbm(formula = medv ~ .,
#                 distribution = "gaussian", #  minimizar erro quadrático
#                 data = conj_treino,
#                 n.trees = 10000,  # número de árvores
#                 interaction.depth = 3,  # profundidade da arvore
#                 shrinkage = 0.1,   # aprendizado rápido
#                 cv.folds = 5, # 5 envelopes de validaçõa cruzada
#                 n.cores = NULL, # 
#                 verbose = FALSE)

Criando um grid para avaliar os parametros e os respectivos RMSEs

hiper_grid <- expand.grid(
  shrinkage = c(.01, .05, .1),
  interaction.depth = c(1, 3, 5, 7),
  n.minobsinnode = c(5, 10, 15),
  bag.fraction = c(.65, .8, 1),
  optimal_trees = 0, 
  min_RMSE = 0   
  )

# numero total de combinações
nrow(hiper_grid)
[1] 108

Avaliando o grid de parametros

# Busca no grid 
for(i in 1:nrow(hiper_grid)) {
  
  # 
  set.seed(21)
  
  # treina o modelo
  gbm.tune <- gbm(
    formula = medv ~ .,
    distribution = "gaussian",
    data = conj_treino,
    n.trees = 6000,
    interaction.depth = hiper_grid$interaction.depth[i],
    shrinkage = hiper_grid$shrinkage[i],
    n.minobsinnode = hiper_grid$n.minobsinnode[i],
    bag.fraction = hiper_grid$bag.fraction[i],
    train.fraction = .75,
    n.cores = NULL, 
    verbose = FALSE
  )
  
 # adiciona os erros de treino e arvores ao grid
  hiper_grid$optimal_trees[i] <- which.min(gbm.tune$valid.error)
  hiper_grid$min_RMSE[i] <- sqrt(min(gbm.tune$valid.error))
}

hiper_grid %>% dplyr::arrange(min_RMSE) %>% head(10)
   shrinkage interaction.depth n.minobsinnode bag.fraction optimal_trees
1       0.10                 1             15         0.65          3074
2       0.10                 1             10         0.65          5262
3       0.05                 1             15         0.80          4392
4       0.10                 1             15         0.80          3321
5       0.05                 1             15         0.65          3074
6       0.05                 1             10         1.00          4455
7       0.10                 1             10         1.00          2073
8       0.10                 1             15         1.00          4124
9       0.05                 1             15         1.00          5996
10      0.05                 5             15         0.65           178
   min_RMSE
1  4.420519
2  4.655791
3  4.667658
4  4.686840
5  4.699871
6  4.775397
7  4.780322
8  4.788251
9  4.818321
10 4.818439

Modelo final

# 
set.seed(21)

# treina o modelo GBM
gbm.fit.final <- gbm(
  formula = medv ~ .,
  distribution = "gaussian",
  data = conj_treino,
  n.trees = 3074,
  interaction.depth = 1,
  shrinkage = 0.10,
  n.minobsinnode = 15,
  bag.fraction = 0.65, 
  train.fraction = 1,
  n.cores = NULL, 
  verbose = FALSE
  )

Variable importance

summary(
  gbm.fit.final, 
  cBars = 13,
  method = relative.influence, # também pode ser usado permutation.test.gbm
  las = 2
  )

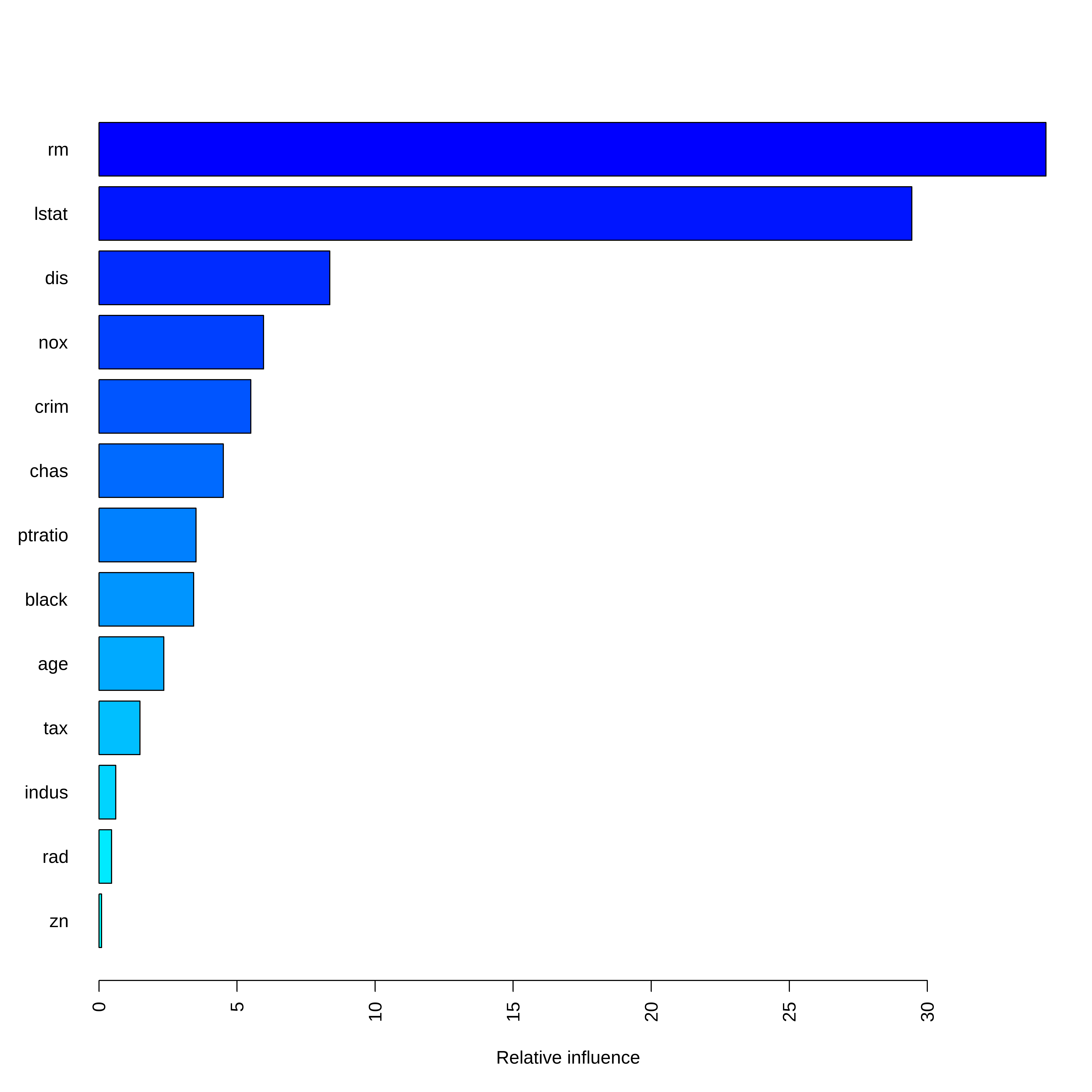
            var    rel.inf
rm           rm 34.2998187
lstat     lstat 29.4374141
dis         dis  8.3574770
nox         nox  5.9614131
crim       crim  5.5011677
chas       chas  4.5023266
ptratio ptratio  3.5157834
black     black  3.4315023
age         age  2.3514968
tax         tax  1.4830798
indus     indus  0.6084729
rad         rad  0.4554056
zn           zn  0.0946421

Previsão

# Fazendo Previsões
previsao1 <- predict(gbm.fit.final, 
                     newdata = conj_teste,
                     n.trees=gbm.fit.final$n.trees)
head(previsao1)
[1] 19.73374 18.76262 19.89281 20.76348 18.34094 16.44815
# Calcula os erros de previsão
caret::RMSE(previsao1, conj_teste$medv)
[1] 4.189849

Entendendo melhor os resultados

library(lime)
model_type.gbm <- function(x, ...) {
  return("regression")
}

predict_model.gbm <- function(x, newdata, ...) {
  pred <- predict(x, newdata, n.trees = x$n.trees)
  return(as.data.frame(pred))
}
# Algumas observações para avaliar
obs_pontuais <- conj_teste[1:2, ]

# aplica o LIME
explicador <- lime(conj_treino, gbm.fit.final)
explicacao <- explain(obs_pontuais, explicador, n_features = 5)
plot_features(explicacao)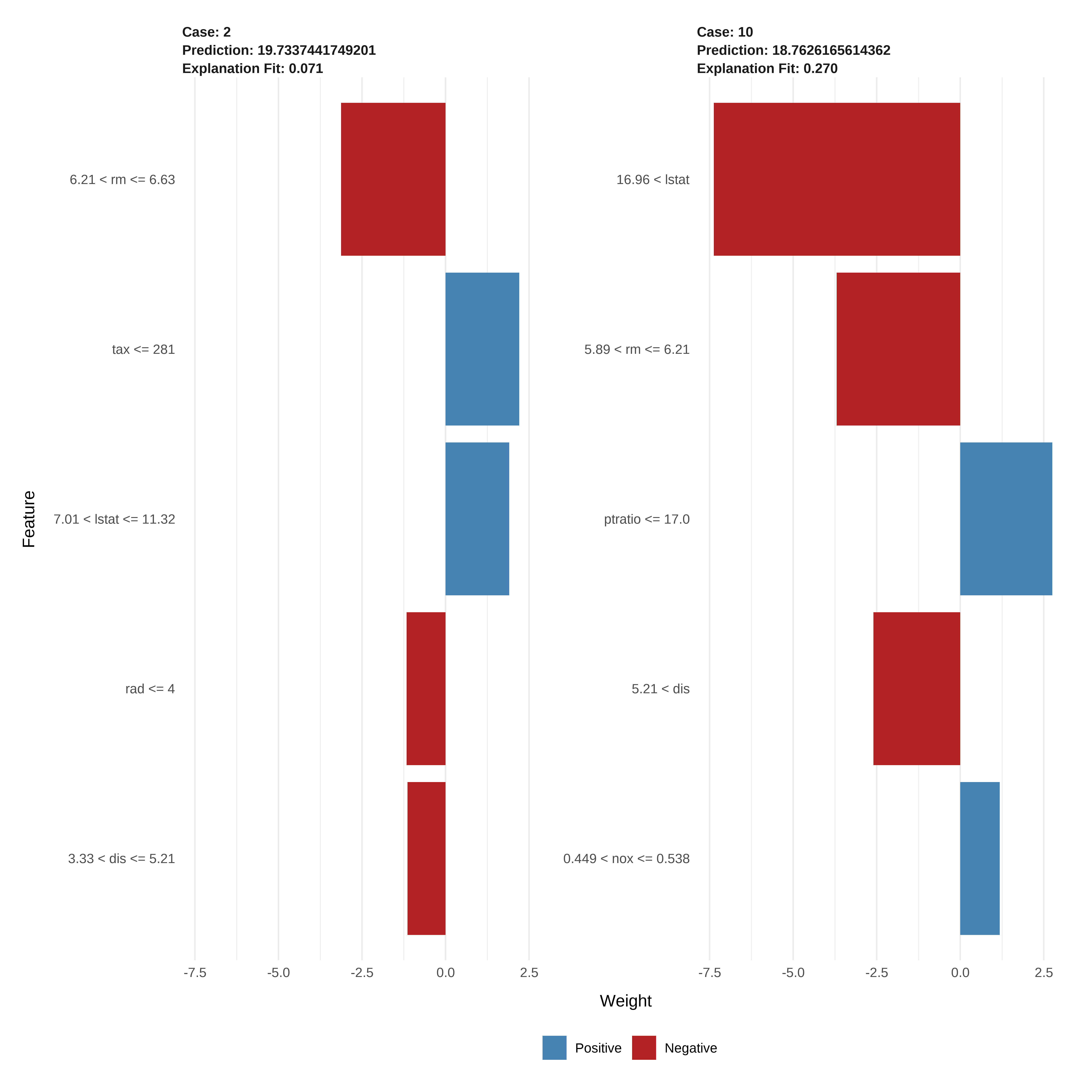

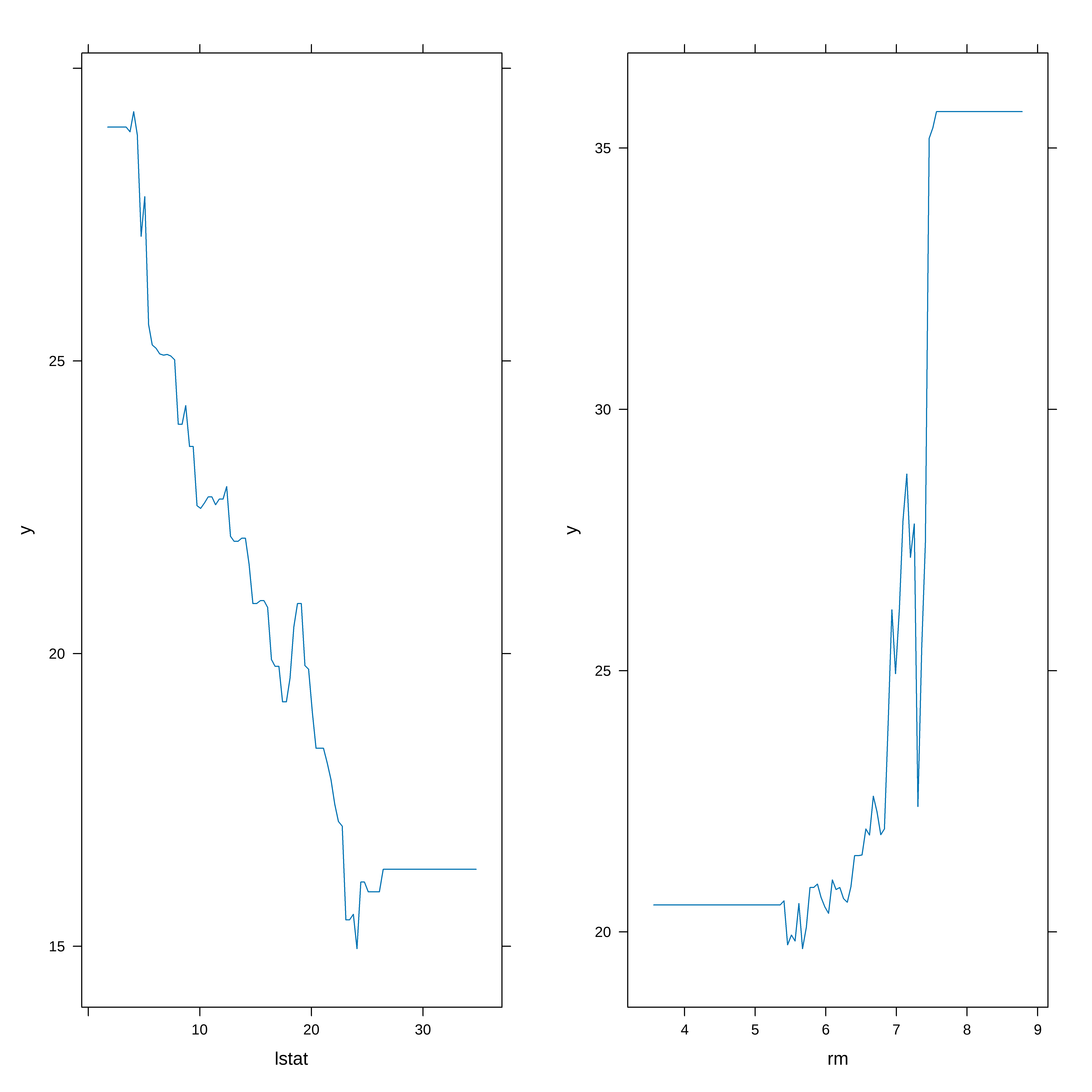
Gráfico de Dependencia Parcial (Partial Dependence Plot)

graf_rm <- plot(gbm.fit.final, i = "rm")
graf_lstat <- plot(gbm.fit.final, i = "lstat")
gridExtra::grid.arrange(graf_lstat, graf_rm, ncol = 2)